Skip to content 
On this page
Algorithm›Basic
Binary Search
本文介绍了整数二分和浮点数二分，以及常用方法。
查找问题
一般实在给定序列中找到符合条件的元素的出现的位置。此类问题的最终的解往往是序列中的某个下标。
例 1 在长度为 10 的随机序列中找到第一个 3 出现的位置，没有则返回-1。
// E1
int a[10] , i; // 数组和下标变量
srand(6); // 设置随机种子
// 填充数组并且查看
for(i = 0 ; i <= 9 ; i++)
{
a[i] = rand() % 10;
cout << a[i] << " ";
}
cout << endl;
// 循序查找 找到输出下标
for(i = 0 ; i <= 9 ; i++)
{
if(a[i] == 3)
{
cout << i << endl;
break;
}
}
// 找不到输出-1
if(i == 10)
cout << -1;二分查找
原理 二分查找运用于有序序列中 将当前区间的中点元素和待查找元素比较 并且根据比较的结果来缩小区间。
这有点类似于猜数游戏。我在 [0 , 100] 之间选定了一个数 ?。第一次不妨猜 50 ，再 根据 50 和 ? 的大小关系来决定下一个猜的数是 25 还是 75。 按照此法最终找到 ?。
注意，我们找到 ? 不是 利用某个数和 ? 相等 来判别的，而是由某一时刻区间无法再缩小来确定的。如果 ? 就是 50 的话 区间会做如下变化
[0 , 100] , [0 , 50] , [25 , 50] , [37 , 50] , ........ [50 , 50] 来最终确定的。
整数二分查找的具体方法
在二分查找中 我会用过一个条件判断来将区间分为两个性质不同的段。
如在 节 2 中，根据和 ? 的大小关系 可以将区间分为。
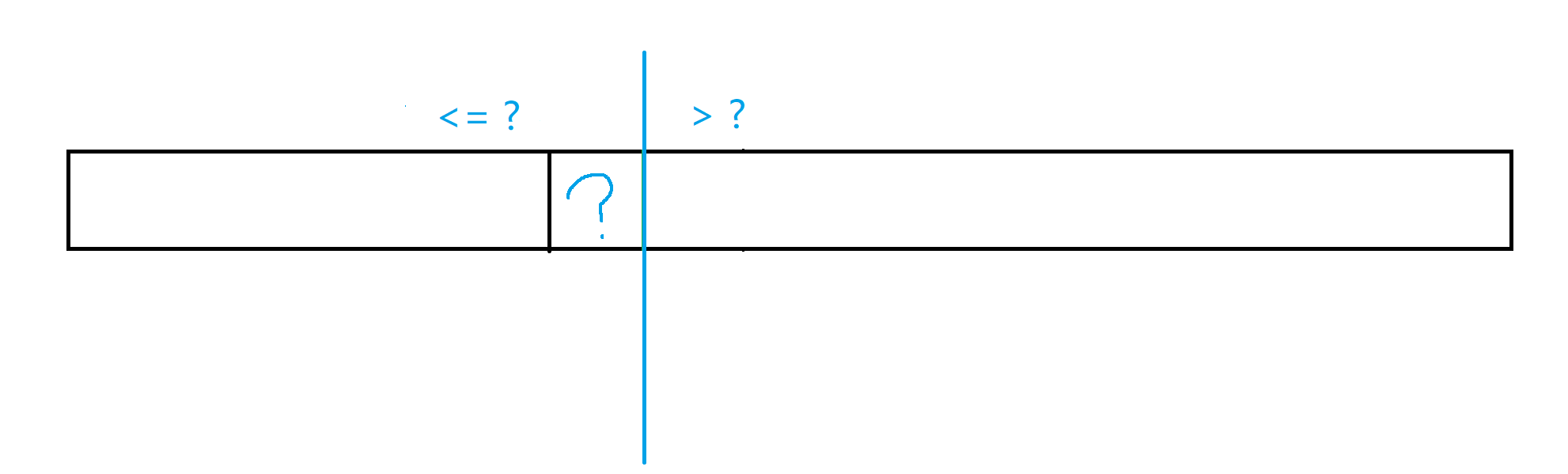
或者
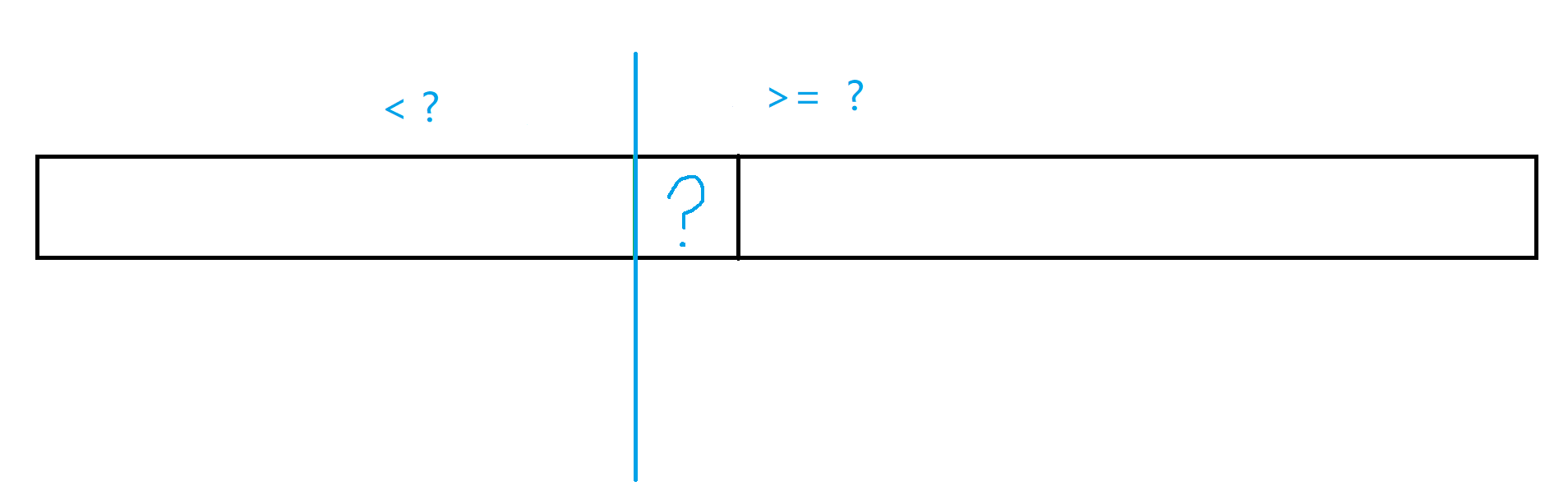
和 ? 的比较方法是在程序里确定的，且只会上图表现的两种中的一种。
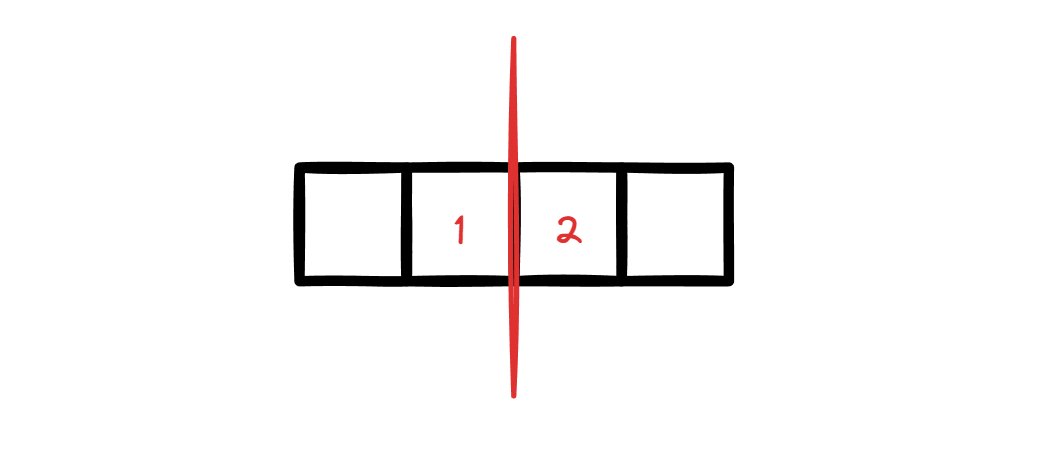
在二分中有意义的结果点有两个，显然是下图中的 1 和 2点。
以此 我们介绍两种二分代码方法。
- 求得 左区间右端点(1 号点)的二分方法
int BinSearch_1(int l , int r)
{
while(l < r)
{
int mid = (l + r + 1) / 2;
if(check(mid)) l = mid;
else r = mid - 1;
}
return l;
}- 求得 右区间左端点的(2 号点)的二分方法
int BinSearch_2(int l , int r)
{
while(l < r)
{
int mid = (l + r) / 2;
if(check(mid)) r = mid ;
else l = mid + 1;
}
return l;
}方法理论
上下中点
观察两种方法中求取中点的不同写法。
int mid = (l + r) / 2;int mid = (l + r + 1) / 2;对于奇数区间，两式求得的位置是一样的。
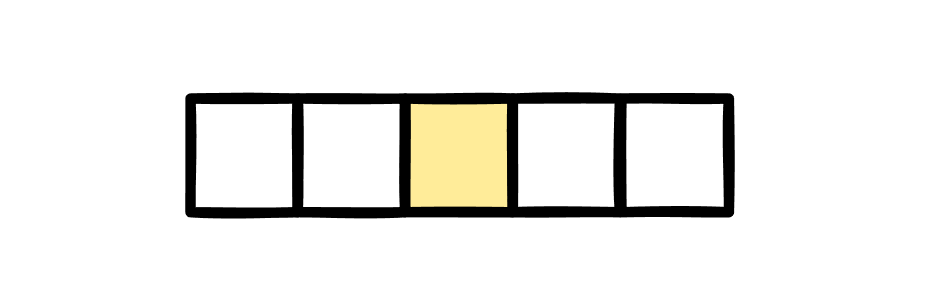
对于偶数区间，两式分别求得上下中点。
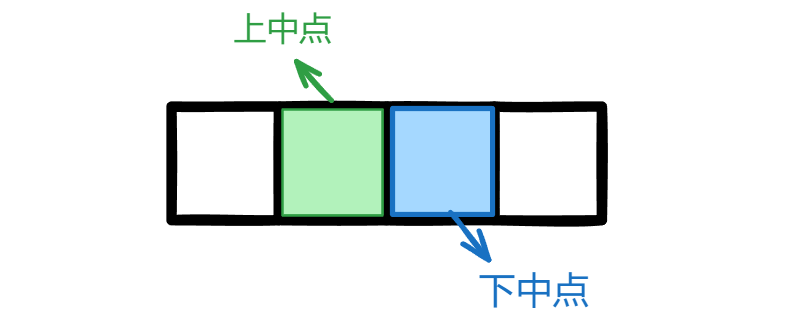
答案
特化一下答案所在的区间。
不难看出，1 号点在左区间中为上中点，2 号点在右区间为下中点。
可出这些原则可以记忆对应的代码:
- 明确所求的点，写对应的取中点方法
- 写
checkmid()时让答案点保持在其区间内- 求 1 号点就检查 mid 是否在左区间，反之同理
- 移动区间端点
- 保持答案在区间内
- 保证区间每次都至少减少 1
一个整数二分的实际问题
- 描述 有一个升序排序的数组
{1 , 2 , 2 , 3 , 3 , 4}。 - 用户给出查询 q 输出 q 在数组中出现的起始位置和结束位置。
- 如果数组中没有 q 则输出
-1 -1。
int a[] = {1 , 2 , 2 , 3 , 3 , 4};
int q;
cin >> q;对于第一个 q 使用节 3 求 2 号点的方法
int l = 0 , r = sizeof(a) / sizeof(int) - 1; // 二分的起始区间 0 - 数组的最后一个下标
while(l < r)
{
int mid = (l + r) / 2;
if(a[mid] >= q) r = mid; // 写目标q(蓝色)所在那部分 即 >= q
else l = mid + 1;
}
if(a[l] != q)
cout << "-1 -1" << endl;对于第二个 q 使用节 3 求 1 号点的方法
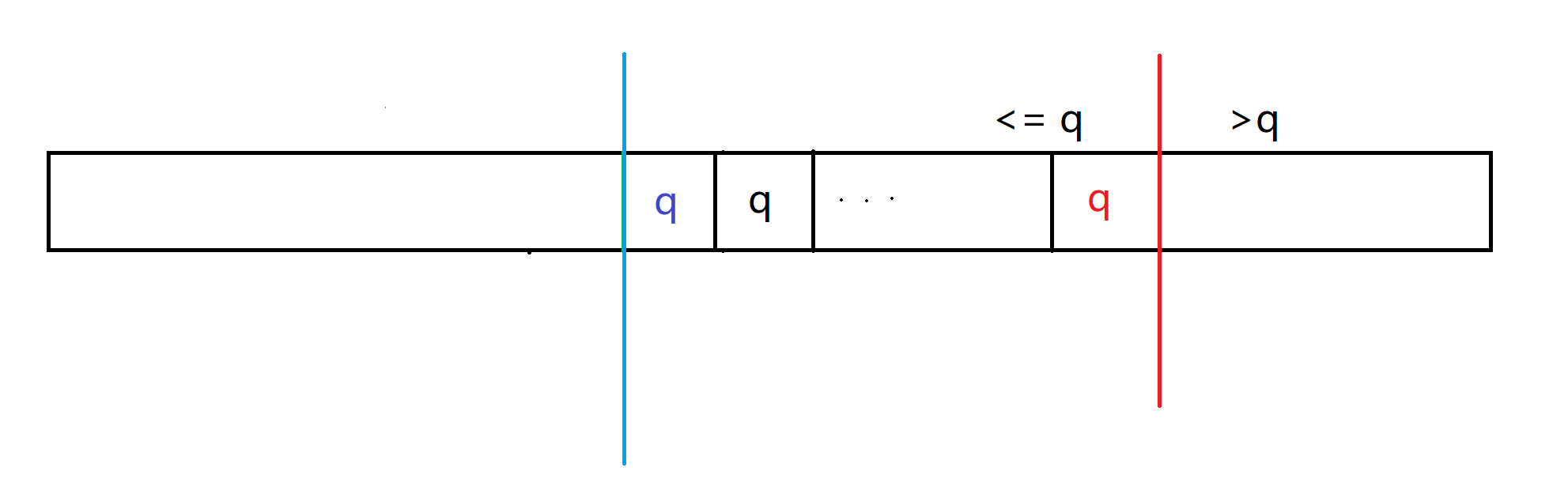
else
{
cout << l << " ";
// 对于最后一个q 依据上法可以分为这样两个区间
// <=q 和 >q 此时要寻找左区间的左端点
l = 0 , r = sizeof(a) / sizeof(int) - 1;
while(l < r)
{
int mid = (l + r + 1) / 2;
if(a[mid] <= q) l = mid; // 写目标q(红色)所在的区间 即 <= q
else r = mid - 1;
}
cout << l << " ";
}5.浮点数二分
- 一个例题
// 使用浮点数二分求0.01的平方根
void Exe1()
{
double l = 0 , r = 1;
while(r - l > 1e-7) // 区别于整数 这里只要左右端点 "足够接近" 即可
{
double mid = (l + r) / 2;
// 这里直接调整左右端点 没有+1的问题
if(mid * mid >= 0.01) r = mid;
else l = mid;
}
cout << l;
}