Algorithm›Basic

High Precision

About 1223 wordsAbout 4 min

基础算法序列

2022-1-13

cover
本文介绍了高精度算法的相关内容。

引言

在 c++中提供了运算符和数据类型来支持我们做运算。

cout << 3 + 5 << endl;

但是 c++中的数据类型在定义时就有固定大小的空间。如 int 为 4 字节 32 为，最大表示范围为

cout << INT32_MAX << endl;

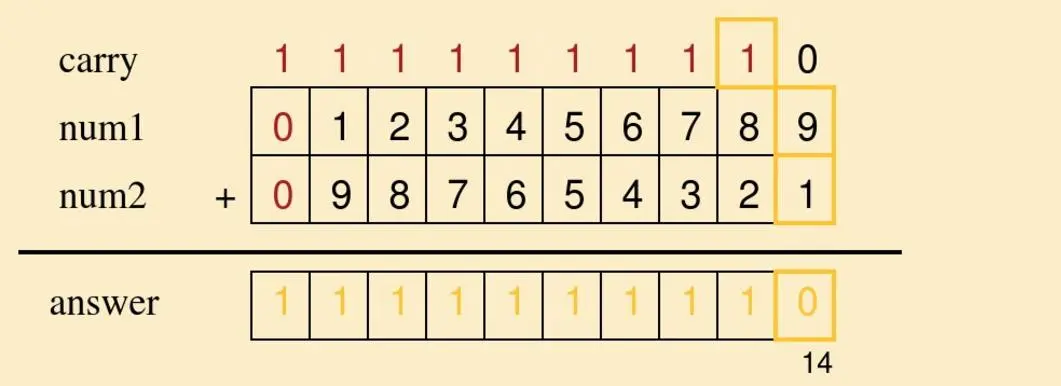
2147483647

高精度算法主要处理以下四类问题

A + B
A - B
A * n
A / n

其中 A , B 的位数 <= 10^6 , n <= 10000

读入和存储

字符串的读入没有长度限制，这里首先读入字符串，再存入向量。

[注: 向量支持动态扩容，相比数组有更好的空间性能]

    string a , b;
    vector<int> A , B;

    cin >> a >> b; // 字符串的读入没有长度限制
    for(int i = a.size() - 1 ; i >= 0 ; i--) A.push_back(a[i] - '0');
    for(int i = b.size() - 1 ; i >= 0 ; i--) B.push_back(b[i] - '0');

另外在数组中采用小端存储的方式，即表现为倒着存储。如读入 123 ，则向量中为

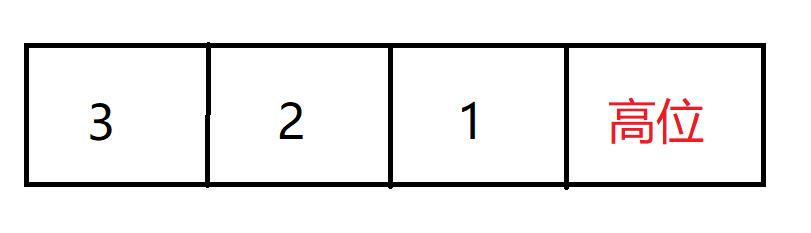
数组存储表示

这是因为如果运算产生进位，那么把它直接加在尾部比较容易。

A + B 问题

vector<int> add(vector<int>& A , vector<int>& B)
{
    vector<int> R;

    int t = 0;
    // 在每一轮开始前 t都是前一位运算结果的进位
    for(int i = 0 ; i < A.size() || i < B.size() ; i++)
    {
        if(i < A.size()) t += A[i];
        if(i < B.size()) t += B[i];
        R.push_back(t % 10); // 将当前位运算结果模10加入结果中
        t /= 10; // 产生下一位的进位
    }
    if(t) R.push_back(1); // 如果最后还有进位 加到结果中

    return R;
}

A - B 问题

在完成 A - B 问题时需要先设计一个函数来比较两数的大小减法算法只处理较大的数减掉较小的数

首先比较数的位数位数长的数大
位数一样的情况下从高位(向量的高端)开始逐位比较位数字大的数大
相等返回 true

bool cmp(vector<int>& A, vector<int>& B)
{
  	// 首先比较长度
    if(A.size() != B.size()) return A.size() > B.size();

    for(int i = A.size() - 1 ; i >= 0 ; i--)
    {
        if(A[i] == B[i]) // 如果两位相等 继续比较下一位
            continue;
        return A[i] > B[i]; // 返回当前位大的数
    }

    return true;
}

接着做减法向加法一样合理处理进位即可

vector<int> sub(vector<int>& A , vector<int>& B)
{
    vector<int> R;

 		// A >= B
    for(int i = 0 , t = 0 ; i < A.size() ; i++)
    {
        // 在循环开始时 t代表上一位的进位 这形成了当前一步的被减数
        t = A[i] - t;
      	// 由于 A >= B 所以要保证减法时 i 对于B不溢出 B[i] 是当前一步的减数
        if(i < B.size()) t -= B[i];
      	// 把相减的结果存入R 如果自然减去后小于零 那么向前借10
        R.push_back((t+10)%10);
      	// 根据是否小于零产生下一步的进位
        if(t < 0) t = 1;
        else t = 0;
    }

    // 去掉多余的零 123 - 120 = 003
    while(R.size() > 1 && R.back() == 0)
        R.pop_back();

    return R;
}

【注: 在输出结果时，如果小数减去大数，则加上负号。】

A * n 问题

在高精度乘法我们处理的问题是一个大数 A 乘一个一般数 n(可以存入 int)

这里我们使用的思想是将 n 视为一个数每次将它和 A 的一位相乘位相乘结果的低位作为结果高位作为进位

vector<int> mul(vector<int>& A , int b)
{
    vector<int> R;
    int t = 0;
    for(int i = 0 ; i < A.size() || t; i ++)
    {
        // 大数没有乘完 或者存在进位t
        if(i < A.size())t += A[i] * b;
      	// 位乘法结果的低一位作为该位的结果
        R.push_back(t % 10);
      	// 高位全部作为进位
        t /= 10;
    }
    return R;

}

A / n 问题

该问题的 A 和 n 的性质同 A * n。

在除法中，我们需要得到商和余数。

// 商为R 余数为r
vector<int> div(vector<int>& A , int b , int& r)
{
    vector<int> R;
    r = 0;
    for(int i = A.size() - 1 ; i >= 0 ; i--)
    {
        r = r * 10 + A[i]; // 和乘法相反 高位留下的数在下一次运算时要乘以10
        R.push_back(r / b); // 结果加上当前位运算的结果 如果不够则直接上0
        r %= b;  // 被除数取模
    }
    reverse(R.begin(), R.end()); // 因为得到的结果 先存储高位再存储低位 这和默认的存储规则相反
    while(R.size() > 1 && R.back() == 0) R.pop_back(); // 去掉高位多余的零
    return R;
}