Presum
本文讲述了基础算法中前缀和和差分的相关内容。
1. 基本概念
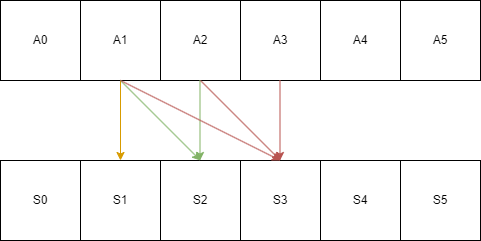
现有一个序列 A1 - An 对应 S1 - Sn 满足以下关系
S1 = A1
S2 = A1 + A2
S3 = A1 + A2 + A3
...
则称 序列 S 为 序列 A 的 前缀和序列 , 而序列 A 为 序列 S 的 差分序列。
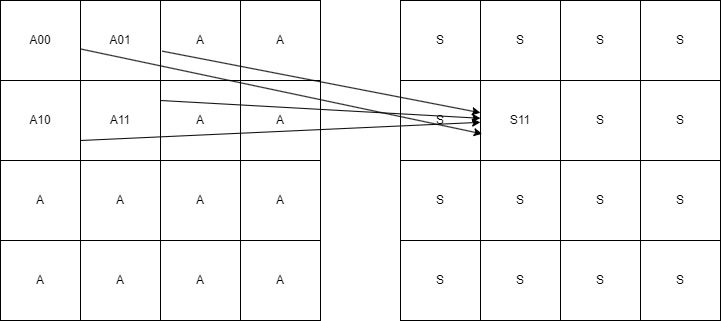
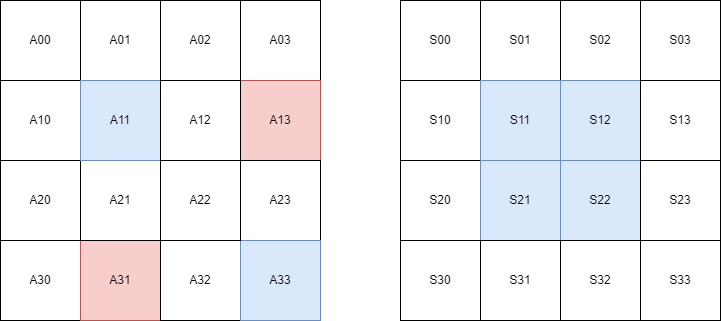
这个概念可以推广到二维序列 如图示
2. 前缀和 , 差分的作用
考虑下面的需求
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问，每个询问输入一对 l,r。
对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。
在朴素的算法中 我们每接受一个输入 都要使用循环扫描[l , r] 将这个区间里的数求一次和。 这样程序核心步骤的运行次数为 m \ avg(r - l)
而如果我们求出了某个序列的前缀和序列 S ，那么求区间[l , r]的和，只要使用 sum(l , r) = S[r] - S[l-1] 。 这样算法核心步骤的运行次数为 n + m。
例如 在图示中 要求 序列 A [4,8] 部分的和 即 A4 + A5 + A6 + A7 + A8。 只需使用 S[8] - S[3]即可。
S[8] = A0 + A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8.
S[3] = A0 + A1 + A2 + A3.
const int N = 100010;
int a[N] , s[N];
void preSum()
{
int n , m;
cin >> n >> m;
for(int i = 1 ; i <= n ; i++) cin >> a[i];
// 前缀和的初始化
for(int i = 1 ; i <= n ; i++) s[i] = s[i-1] + a[i];
// 区间和的计算
while(m--)
{
int l , r;
cin >> l >> r;
cout << s[r] - s[l-1] << endl;
}
}我们在使用前缀和和差分处理问题要把握住这个思想 -- 将线型问题缩小到某几个点上处理。
3.二维前缀和
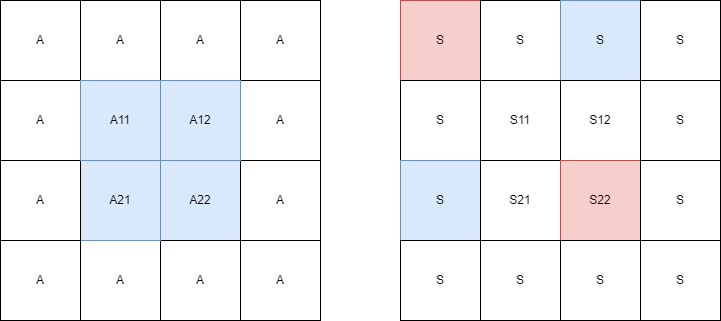
在二维前缀和的运用中 类比一维前缀和 需要掌握两个公式
- 二维前缀和的计算
S[i][j] = S[i-1][j] + S[i][j-1] + A[i][j] - S[i-1][j-1]
- 求
(x1 , y1) -- (x2 , y2)的方形区块内的和 sum(A[x1][y1]-A[x2][y2]) = S[x2][x1] - S[x2][y1-1] - S[x1-1][y2] + S[x1-1][y1-1]
const int N =1010;
int a[N][N] , s[N][N];
void preSum2D()
{
/*
第一行包含三个整数 n，m，q。
接下来 n 行，每行包含 m 个整数，表示整数矩阵。
接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。
*/
int n , m , q;
cin >> n >> m >> q;
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
cin >> a[i][j];
// 二维前缀和的计算
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
s[i][j] = s[i-1][j] + s[i][j-1] + a[i][j] - s[i-1][j-1];
int x1 , y1 , x2 , y2;
while(q--)
{
// 通过前缀和矩阵计算某一区块的面积
cin >> x1 >> y1 >> x2 >> y2;
cout << s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1] << endl;
}
}4 . 差分
在 1 中知道，差分序列的前缀和序列是一一对应的，而我们构造这两个序列的目的，是将需要通过循环处理的操作通过其对应序列上的几点来完成。
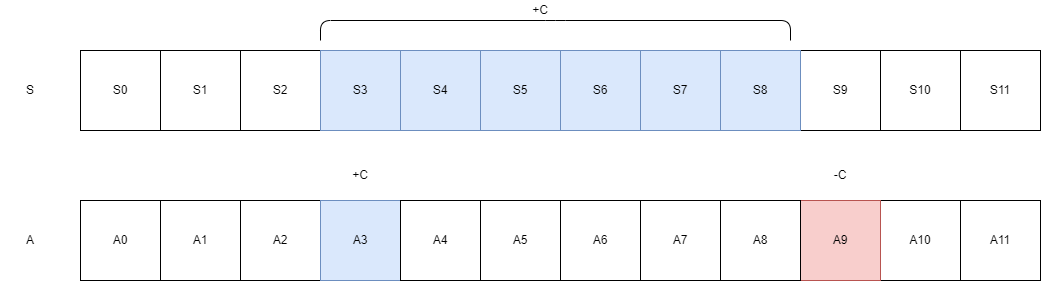
现有一个长度为 n 的整数序 S，并且要需要在序列的[L,R]段上加上 C。这个操作要重复许多次。借用上述思想来处理该问题。
- 首先将该序列视为某个差分序列的前缀和序列 将原序列记为 A
- 在 S 的某段
[L , R]加上C相当于在其原序列的L位置加上C在原序列的 R+1 位置减掉C
const int N = 10010;
int S[N] , A[N];
void insert(int l , int r , int c , int A[])
{
A[l] += c;
A[r+1] -= c;
}
void diff()
{
/*
第一行包含两个整数 n和m。
第二行包含 n个整数，表示整数序列。
接下来 m行，每行包含三个整数 l，r，c，表示一个操作。
*/
int n , m;
cin >> n >> m;
// 一个差分集合和前缀和集合是等价的。
// 在前缀和集合的一段[l , r]上 做操作c
// 相当于在差分上做 s[l]+c , s[r+1]-c
for(int i = 1 ; i <= n ; i++)
cin >> S[i];
// 将S视为某个前缀和结合，那么为其构造一个差分集合A
// 这里的做法是 首先将S试做全零 接着在[1,1] [2,2]...[n,n]区间上插入S数组对应的数
// 在A数组上其相应的操作
for(int i = 1 ; i <= n ; i++)
insert(i , i , S[i] , A);
// 在这个查分集合上做操作
int l , r , c;
while(m--)
{
cin >> l >> r >> c;
insert(l , r , c , A);
}
// 将A还原为S
// A为查分集合 S为其前缀和
for(int i = 1 ; i <= n ; i++)
S[i] = A[i] + S[i-1];
// 输出S的全部元素
for(int i = 1 ; i <= n ; i++)
cout << S[i] << " ";
cout << endl;
}5. 二维差分
也是将差分推广到二维。在二维差分中，在前缀和矩阵的某个子矩阵{[x1,y1] - [x2,y2]}中进行+C 操作，相当于在其差分矩阵中做
- [x1 , y1] += C
- [x1 , y2+1] -= C
- [x2+1 , y1] -= C
- [x2+1 , y2+1] += C
const int N = 1010;
int S[N][N] , A[N][N];
void insert2D(int x1 , int y1 , int x2 , int y2 , int c)
{
A[x1][y1] += c;
A[x1][y2+1] -= c;
A[x2+1][y1] -= c;
A[x2+1][y2+1] += c;
}
void diff2D()
{
/*
第一行包含整数 n,m,q。
接下来 n行，每行包含 m个整数，表示整数矩阵。
接下来 q行，每行包含 5个整数 x1,y1,x2,y2,表示一个操作。
*/
int n , m , q;
cin >> n >> m >> q;
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
cin >> S[i][j];
// 将S视为某前缀和矩阵 A为其差分矩阵 差分矩阵的构造方法如下
// 在前缀和矩阵的 (x1 , y1) , (x2 , y2)之间做操作c
// 相当于在其差分矩阵上 1.在(x1 , y1) 出加上c 2.在(x1 , y2+1)减掉c 3.在(x2+1 , y1)处减掉c
// 4.在(x2+1, y2+1)处加上c 可以以此构造insert函数
for(int i = 1 ; i <= n; i++)
for(int j = 1 ; j <= m ; j++)
insert2D(i , j , i , j , S[i][j]);
// 读入并做操作
int x1 , y1 , x2 , y2 , c;
while(q--)
{
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert2D(x1 , y1 , x2 , y2 , c);
}
// 将差分还原为前缀和矩阵
for(int i = 1 ; i <= n ; i++)
for(int j = 1; j <= m ; j++)
S[i][j] = S[i-1][j] + S[i][j-1] + A[i][j] - S[i-1][j-1];
// 输出S矩阵
for(int i = 1 ; i <= n ; i++)
{
for(int j = 1 ; j <= m ; j++)
cout << S[i][j] << " ";
cout << endl;
}
}版权所有
版权归属：