Algorithm›Basic

Sort Algorithms

About 835 wordsAbout 3 min

2022-1-10

cover
本文讲解了快速排序和归并排序的实现方法。

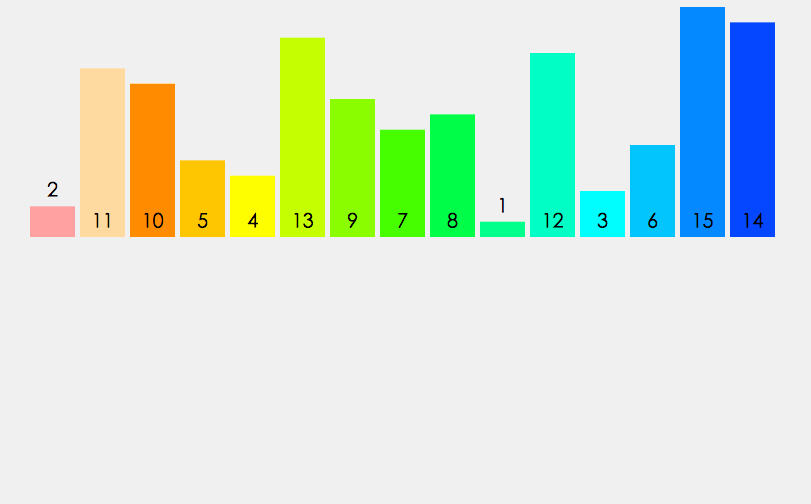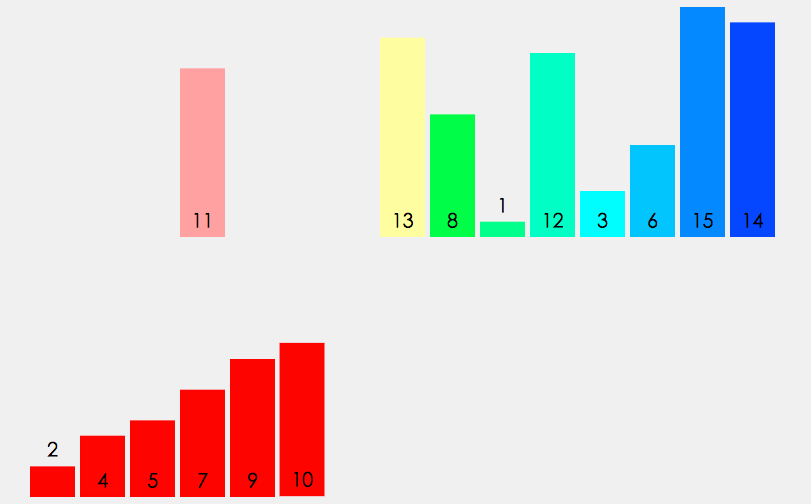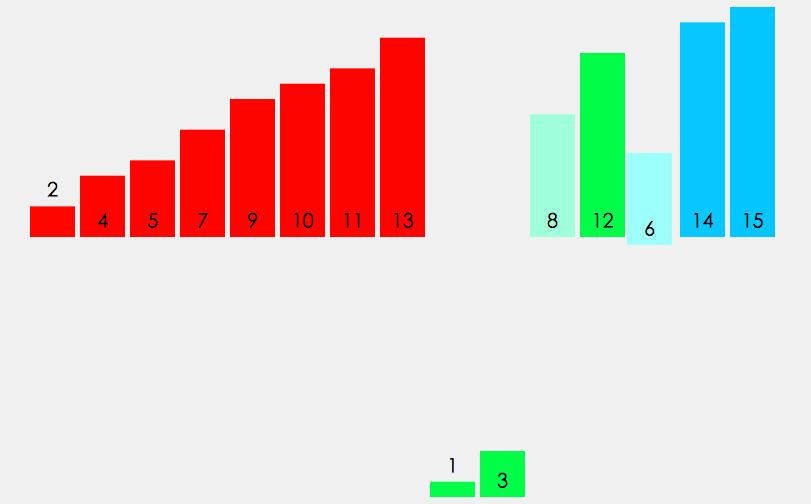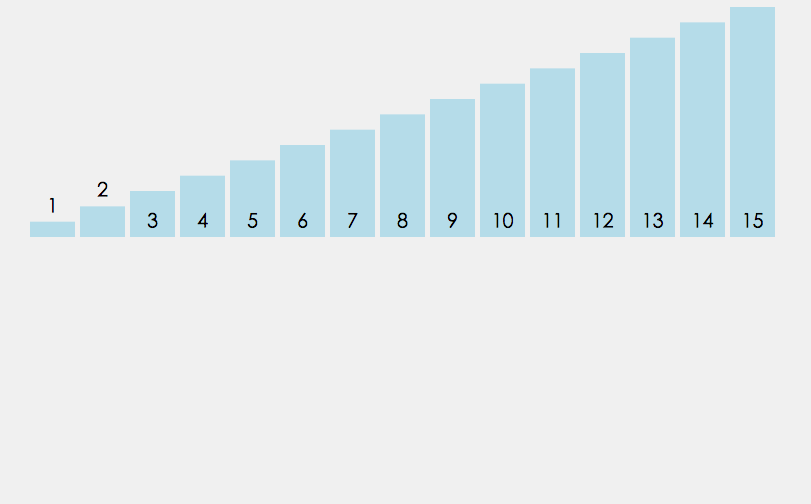
快速排序

快速排序基于分治思想可以分为三个步骤

选定分界点可以取两端点中点或随机点
使用一个特定分割方法进行数组分割
对子数组递归的使用快排

快排可以是稳定的，取决于具体的做法。下面将列举一些常见的快排做法(主要是分割数组的方法不同)，并对它们进行数组分割。

快慢指针

void QuickSort(int a[] , int start , int end)
{
    if(start >= end) //终止条件
        return;
    int p = a[end]; // 分割点
    int i = start , j = start; // 快慢指针
    for( ; j < end ; j++) // 快指针前进搜索 start ~ end-1
    {
        if(a[j] <= p)
        {
		    if(i != j)
	            swap(a[i++] , a[j]); // 将小元素交换给慢指针
	        else
		        i++;
        }
    }
    swap(a[i] , a[end]); // 交换慢指针所在位置和分割点
    QuickSort(a , start , i-1); // 对两端区间分别做快排
    QuickSort(a , i+1 , end);
}

快慢指针的大体思想是利用快指针将后方大的元素移动到前方
使用该方法进行分割在数组有序的前提下整个快排的复杂度会退化到O(0.5 * n^2)
- 递归树每次只能排除一个元素递归树往单边生长

优化

任何选取区间端点作为分割元素的方法都不可避免的会有递归树倾斜和复杂度退化的问题。这些可以采用区间中间作为分割元素。

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }

    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

注意

这显然是一种应试主义，我们可以构造一种输入，使得该方法的递归树也出现倾斜。

归并排序

归并排序同样基于分治思想

分割序列直到每个序列长度为 1 此时每个子序列是有序的
- 先分割意味着递归在代码的前部
接着不断合并有序数组直到整个数组都有序

void MergeSort(int a[] , int start , int end)
{
    if(start >= end) // 终止条件
        return;

    // 分割区间
    int mid = (start + end) / 2;
    MergeSort(a , start , mid);
    MergeSort(a , mid+1 , end);

    // 在运行到这一步时 start-mid , mid+1 - end 分别为两段有序序列
    int t[end - start+1] , i = 0; // 临时数组和插入位置指针
    int l = start , r = mid+1; // 左右子数组中的指针

    // 合并
    while(l <= mid && r <= end)
        t[i++] = a[l] < a[r] ? a[l++] : a[r++];
    while(l <= mid)
        t[i++] = a[l++];
    while(r <= end)
        t[i++] = a[r++];

    // 将临时数组的内容写回原数组
    for(i = 0 ; i < end-start+1 ; i++)
    {
        a[start + i] =  t[i];
    }
}