01 Bag
这篇文章对01背包已经优化做了详细解读。
0-1 背包问题
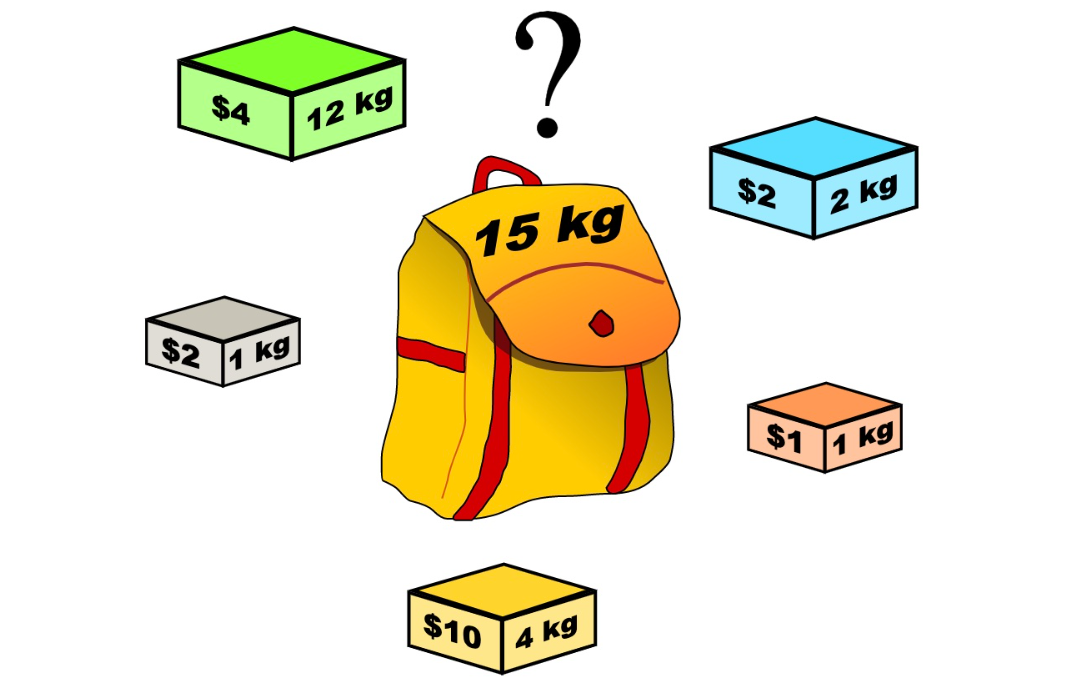
01 背包考虑使用诺干具有一定体积和价值的物品填充一个固定价值的背包，求解一个最大价值的装填方案。
试一试
DP 表
DP 表图解
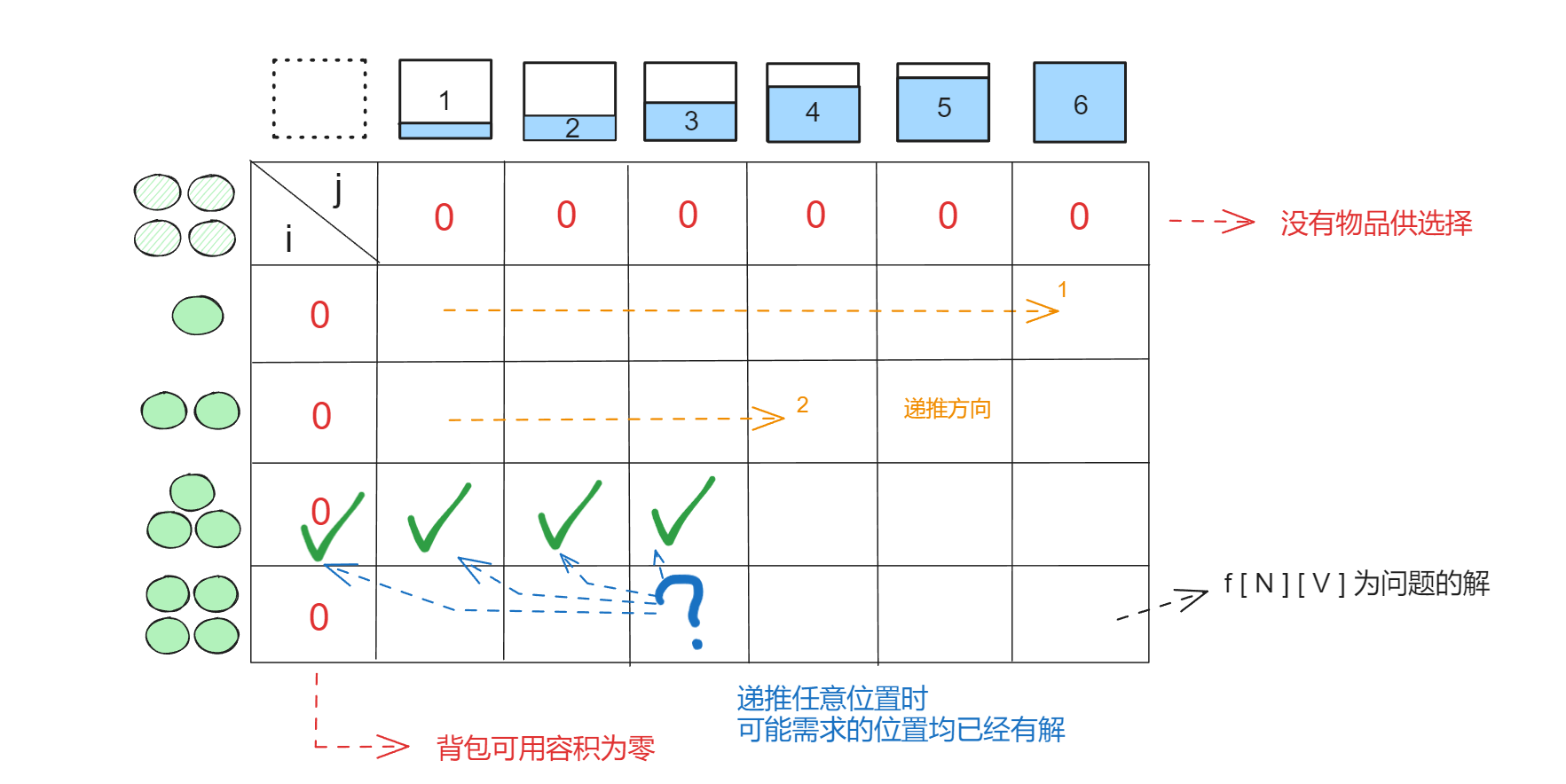
递推过程
- 创建 dp 表格 大小为
(N+1)*(V+1),f[i][j]代表选择前i个物品填充容量为j的背包时问题的解(这个情况下的最大价值)。 - 将
i == 0的行 和j == 0初始化为0。i == 0代没有物品可供选择，j == 0代表背包容量为零，故这些子问题的答案都为零。 - 逐行逐列进行递推，方见图中的橙色箭头, 在这种递推方式下，可能用到的子问题的解均已经在之前的过程求出。
- 答案存储在表格的右下角位置，即
f[N][V]的位置。
递推式
必须要思考一个问题，状态是如何转移的。一般来说我们考虑离位置点最近的一些状态。 现在我们要递推一个 新的 f[i][j] , 这个位置的左边位置是f[i-1][j], 上边位置是 f[i][j-1]。 我们可以从其左边位置考虑，先让
f[i][j] = f[i-1][j];这样做的语义是 如果不选择 第 i 个物品装入背包，那么 f[i][j] 的答案 和 f[i][j-1]的答案是相同的。
这样做显然没有考虑所有的情况，进一步的，我们考虑如果将第 i 个物品放入背包可以对递推的过程进行补充。
- 如果物品体积小于当前子问题背包容量
j，才可以放入。 - 放入后的背包剩余容量为
j - weights[i]，这个剩余容量仍可能装入一些其他物品。 - 加入第
i个物品的操作使得背包的价值增加了values[i]。 - 考虑这样相比如不加入第
i个物品能否得到一个更大的背包总价值。
if(j > weights[i]) f[i][j] = max(f[i][j] , f[i-1][j-weights[i]] + values[i]);全部代码
#include<iostream>
using namespace std;
const int N = 1e3 + 10;
int weights[N] , values[N];
int f[N][N];
int main()
{
int N , V; cin >> V >> N;
for(int i = 1 ; i <= N ; i++)
cin >> weights[i] >> values[i];
for(int i = 1 ; i <= N ; i++)
{
for(int j = 1 ; j <= V ; j++)
{
f[i][j] = f[i-1][j];
if(j >= weights[i]) f[i][j] = max(f[i][j] , f[i-1][j-weights[i]] + values[i]);
}
}
cout << f[N][V];
}优化
01 背包可以对空间存储进行优化。观察这个递推局部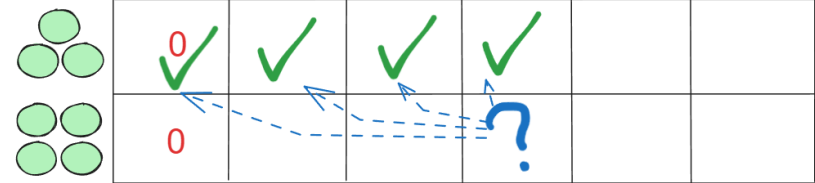 
可以看出，递推一个新的位置 f[i][j], 只需要 利用 f[i-1][0] - f[i-1][j]。所以当我们在一行内进行递推时，在递推下一行时
f[i][j]被默认初始化为了 f[i-1][j]。为了计算得到正确的 f[i][j], 必须在新行内从后往前进行递推。在递推时，只需要递推到 weight[i]即可结束。
优化代码
#include<iostream>
using namespace std;
const int N = 1e3 + 10;
int weights[N] , values[N];
int f[N];
int main()
{
int N , V; cin >> V >> N;
for(int i = 1 ; i <= N ; i++)
cin >> weights[i] >> values[i];
for(int i = 1 ; i <= N ; i++)
{
for(int j = V ; j >= weights[i] ; j--)
{
f[j] = max(f[j] , f[j-weights[i]] + values[i]);
}
}
cout << f[V];
}复杂度分析
- 时间复杂度为
O(N * V) - 空间复杂度为
O(V)
版权所有
版权归属：