Concepts About Dynamic Programming
这篇文章介绍了动态规划的概念和划分方法。
前言
阅读本文之前，需要先阅读递归和递推,这有助于更好的理解本文的内容。
在动态规划的一个章节，我们参考《算法竞赛进阶指南》中关于动态规划的讲解，把动态规划的几个核心概念梳理一下，并做一个总结。
在后续动态章节中，会对动态规划每个类型的经典问题做出讲解，大家可以在一定程度的学习之后再回头阅读总结，相信会有更深刻的认识。
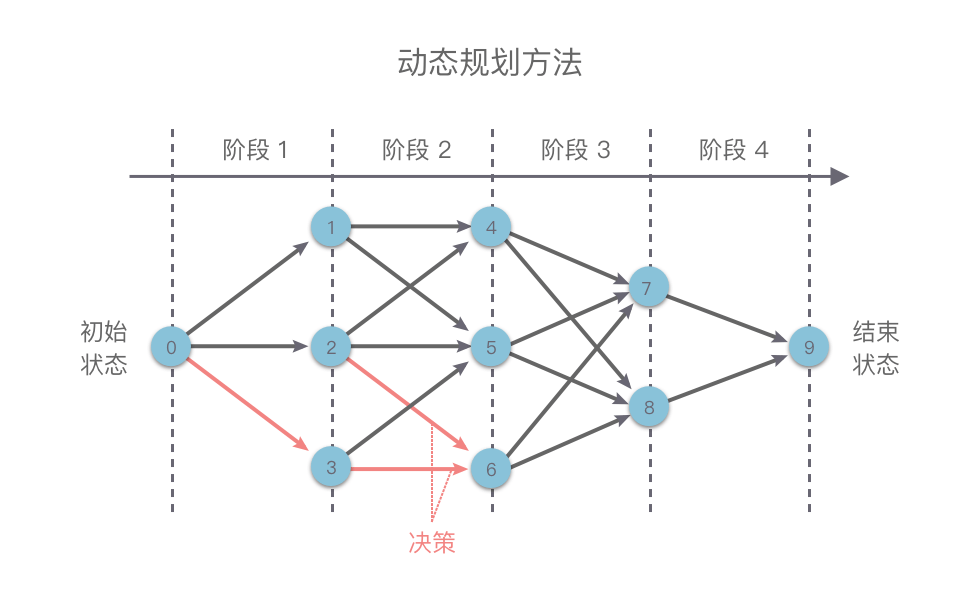
下文涉及的概念可以借助下图归纳: 
动态规划概念
下面将以书中的范式来解读的动态的概念和过程，这些概念可以帮助大家建立对动态规划的理解。
阶段
动态规划把原问题视为若干个重叠子问题的逐层递进，每个子问题的求解过程都构成一个阶段。在完成前一个阶段的计算后，才会执行下一阶段的计算。
无后效性
在 dp 求解的过程中，在完成前一个阶段的计算后，才会执行下一阶段的计算，换句话说，一个新问题所依赖的子问题都必须是全部有解的。大家在背包相关问题，区间 Dp 相关问题的推导图解可以更清楚的看明白这一点。
为了保证这些计算能够按顺序，不重复地进行，DP 要求已经求解的子问题不受后续阶段的影响。(后面的阶段对前面的阶段没有影响)。
状态，转移和决策
无后效性。DP 对状态空间的遍历构成 DAG，遍历顺序就是该 DAG 的一个拓扑序。DAG 中的节点对应问题的状态，边对应状态之间的转移，转移的选取是 DP 中的决策。
最优子结构,重复子问题
最优子结构: 当动态规划用于求解最优化的问题时，下一阶段的最优解应该能由前面各阶段子问题的最优解导出。
在阶段计算完成的时候，只会在每个状态上保留与最终解集相关的代表信息，这些信息具有可重复的求解过程，并且能够导出后续阶段的代表信息。这样，动态规划对状态的抽象和子问题的重叠递进共同起到优化作用。
状态转移方程
动态规划算法把相同的计算过程作用于各阶段的同类子问题，我们一般只需要定义出 DP 的计算过程即可，这个计算过程称为状态转移方程。
状态转移方程一般可以有两种思考方式：
- 当前状态可以从哪些状态转移过来。
- 当前状态可以转移到哪些状态。
总结
状态，阶段，决策是动态规划算法的三要素。
无后效性，最优子结构，重复子问题是问题能用 DP 求解的三个基本条件。
对具体问题，可以按以下流程分析，难点在于如何把问题形式化为状态空间，进一步抽象出 DP 的状态表示和阶段划分：
- 找到重复子问题，最优子结构；
- 根据子问题的求解过程明确阶段划分；
- 根据由上一阶段的结果计算当前阶段时所需的信息，抽象出状态表示，如果阶段不足以表示一个状态，需要把附加信息也作为状态的维度；
- 由子问题的重叠递进的方式，设计状态转移方程，并给出边界，目标；
经过以上分析后，最终算法呈现出来的事状态设计、边界值、目标、状态转移方程四部分。其中状态设计中除了划分阶段的维度，还可能有附加信息的维度。
给出了状态转移的方程、边界和目标，一个动态规划的问题就算是解决了，程序实现可能会有些细节，但是是小问题。
阶段的划分方式
动态规划是对各维状态进行分阶段，有顺序，无重复，决策性的遍历求解，
不同问题的动态规划算法有不同的阶段划分和推导的方式，常见的阶段划分方式如下:
- 线性 DP: 具有线性阶段划分的 DP 问题。
- 树形 DP: 以节点的深度作为阶段的 DP 问题。
- 图上 DP: 以节点在图上的拓扑序作为阶段的 DP 问题。