Interval DP
这篇文章介绍了动态规划的概念和划分方法。
前言
在阅读本文之前，你需要阅读动态规划概念和线性动态规划。这有助于你更好的理解本文的思想。
本质不同
递推顺讯
在线性动态规划中，我们在 dp 表中递推顺讯为按行按列递推。在一维输入，递推顺序为。
在二维输入中，递推顺讯为
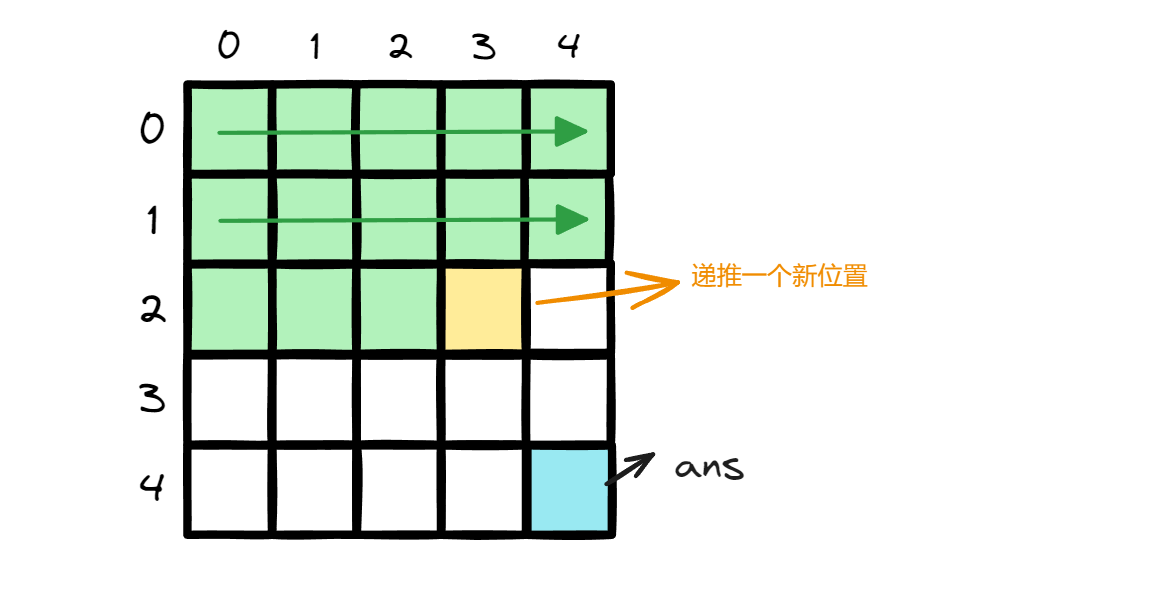
区间 dp
在区间 dp 中，往往我们递推一个二维的 dp 表格。而我们递推原则是从小的区间递推至大的区间，最终的答案存储在表示整个区间的状态中,例如f[1][N]位置。
例题 石子合并
试一试
状态表示
int f[N][N] , f[i][j] 表示合并区间[i , j]内所有石子的最小代价。
初始化
- 因为求取的是最小值，将整个
f数字初始化为INF。 - 将
f[i][i]初始化0,因为合并一堆石子不需代价。
递推
顺讯
枚举所有的区间长度，从长度为 2 开始 , 到长度为 n结束 。再枚举所有的起点，以真的得到这些区间。
对于一个新的位置 f[i][j] , 考虑其最后一次合并的情况。换言之，考虑将这堆石子分成左右两份会有哪些情况。显然，共有 j - i 中情况，其可能分割的点数量为区间长度减一。
递推式
因为所有更小的区间已经有解，而合并任意stones[i][ki] 和 stones[ki+1][j]的代价都是固定的，因为合并前是左右两堆，所以任意一种分割方式的合并代价都是左边区间的石子数量+右边区间的石子数量，也即是这堆石子的总数量，sum(stones[i] , stones[j])。
所以f[i][j] 求解时选择 f[i][ki] + f[ki+1][j]最小的哪个即可。
f[i][j] = min(f[i][j] , f[i][ki] + f[ki+1][j] + sum(stones[i] , stones[j]));答案
答案在f[1][n]位置，表示合并石子区间[1 , n]的最小代价。
完整代码
#include<iostream>
#include<cstring>
using namespace std;
const int N = 310;
int stones[N] , presum[N] , f[N][N];
int main()
{
int n; cin >> n;
for(int i = 1 ; i <= n ; i++)
{
cin >> stones[i];
presum[i] = stones[i] + presum[i-1];
}
memset(f , 0x3f , sizeof f);
for(int i = 1 ; i <= n ; i++) f[i][i] = 0;
for(int len = 2 ; len <= n ; len++)
{
for(int start = 1 ; start + len - 1 <= n ; start++)
{
int end = start + len - 1;
for(int k = start ; k <= end - 1 ; k++)
{
f[start][end] = min(f[start][end] , f[start][k] + f[k+1][end] + presum[end] - presum[start-1]);
}
}
}
cout << f[1][n];
}版权所有
版权归属：