这篇文章介绍了动态规划的概念和划分方法。

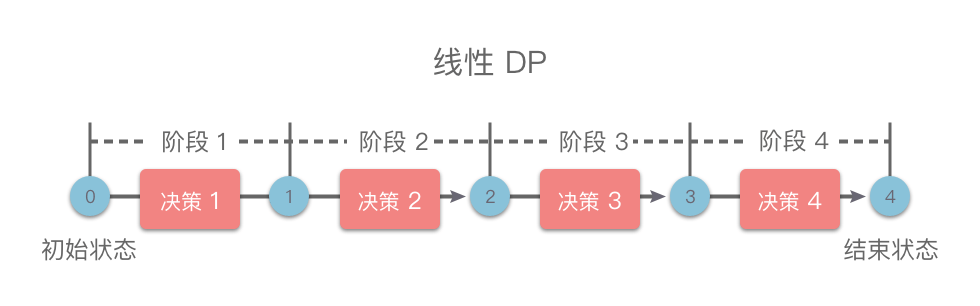
线性 DP 概念

线性 DP : 具有线性阶段划分和推导的 DP 问题。

这是一个广义的概念，与线性空间类似，如果一个 DP 算法的状态包含多个维度，但是各个维度上具有线性变化的阶段，也是线性 DP，例如背包问题，区间 DP 均属于这种情况。

前文写的为广义的定义，而现在背包问题，区间 DP 等往往作为单独的板块来研究。在本文中，我们只讨论输入为一维和二维的经典递推问题。

首先于篇幅， 请大家在试一试中查看题目的具体细节。

一维输入

单串阶段划分

打家劫舍

状态表示

和houses等长的 dp 数组f,f[i] 表示小偷偷窃到第i间房屋时可以偷窃得到的最大金钱。

递推

考虑是否偷窃第 i 间房屋，如果偷窃，那么第 i - 1间房屋则不能被偷取，此时偷得的最大金额是 f[i-2] + houses[i]。如果不偷盗第 i 间房屋，那么可以偷得的最大金额是f[i-1]递推时取二者的较大值。

f[i] = max(f[i-1] , f[i-2] + houses[i]);

优化

由于在递推一个新位置时，只需要用到前两个位置对应的子问题答案，所以只需要使用两个额外空间即可。

完整代码

#include<iostream>
using namespace std;

const int N = 1e6;
int houses[N];
long long pre1 , pre2;

int main()
{
    int n; cin >> n;
    for(int i = 1 ; i <= n ; i++) cin >> houses[i];

    pre1 = max(houses[2] , houses[1]) , pre2 = houses[1];

    for(int i = 3 ; i <= n ; i++)
    {
        int cur = max(houses[i] + pre2 , pre1);
       	pre2 = pre1 , pre1 = cur;
    }
    cout << pre1;
}

最长上升子序列(LIS)

状态表示

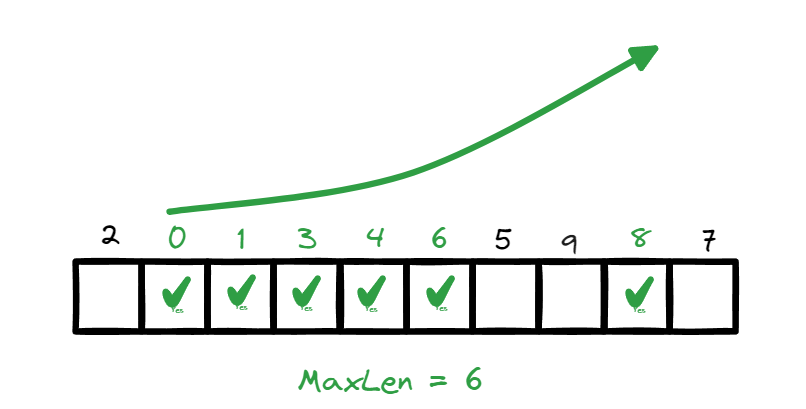
和输入序列a等长的 dp 数组f, f[i]表示以a[i]结尾的最长上升子序列的长度。

注意

• 子序列不一定是原序列中连续的一段。
• 最长的子序列不一定以a的最后一个元素结尾,意味着答案是f中的最大值。

状态转移

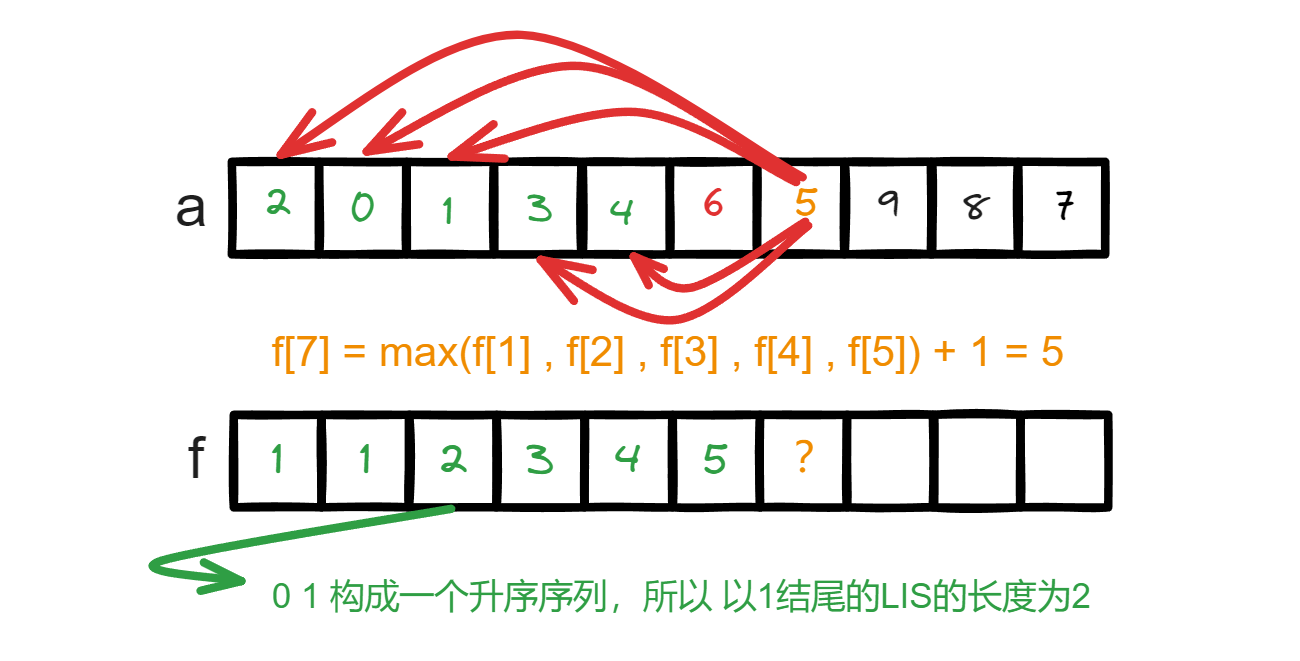
当递推计算一个新状态f[i]时,在a[1] - a[i-1]中找比a[i]小的数字，将接驳产生的序列的长度最大值作为新状态f[i]的答案。

完整代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;
int a[N] , f[N];

int main()
{
    int n ; cin >> n ;
    for(int i = 1 ; i <= n ; i++) cin >> a[i];

    f[1] = 1;
    int ans = 1;
    for(int i = 2 ; i <= n ; i++)
    {
        int m = 0;
        for(int k = 1 ; k < i ; k++)
        {
            if(a[i] > a[k])
                m = max(m , f[k]);
        }
        f[i] = m + 1;
        ans = max(ans , f[i]);
    }
    cout << ans;
}

最长上升子序列(二)

条件

和原问题相比，N的范围由1e3 提高至 1e5 , O(N^2)的算法会导致超时。

新的方法

使用多个单调队列记录每个长度的末尾元素。 在一个新元素到来时，考虑更新这个队列。

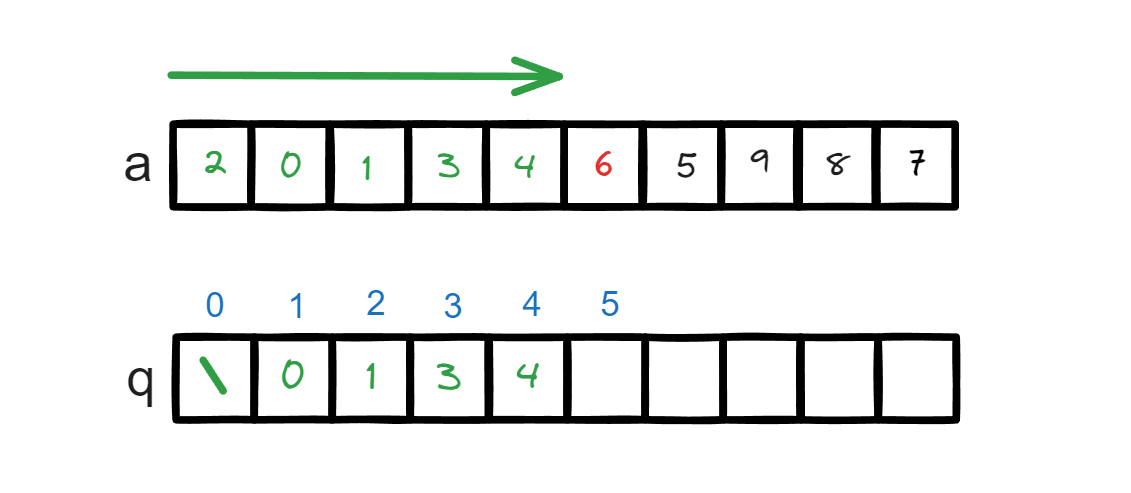
说明

• q是一个单调队列，q[i]表示长度为i的上升子序列的结尾元素。
• q[1] 有五个选择， a[1] - a[5]都可以是其备选，因为一个元素总是合法的 LIS。但我们总是取所有可能选择中结尾最小的那个，即是a[2]为0。因为这样可以再后续的遍历中接续更多的元素，或者说，其他元素可以产生的序列，替换为该最小元素也一样可以产生。
• 同样的 长度为 2 的序列有[2 , 3] , [0 , 1] , [0 , 3] , [0 , 4] , [3 , 4] , [1 , 3] , [1 , 4]选取其中最小的元素1作为q[2]的记录元素。

队列的延伸

考虑如何处理一个新的元素，现在需要处理a[6] = 6, 现在所有的记录中，没有比6 大的记录，所以6可以接续在长度为 4 的序列后，得到长度为 5 的序列。记录q[5] = 6。

队列的更新

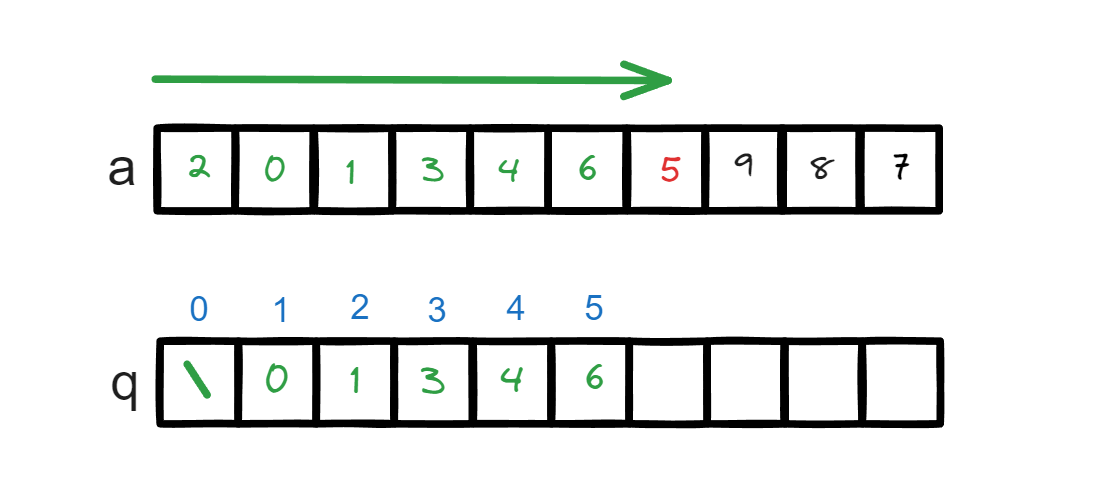
现在考虑一个新元素 5 , 该元素无法得到一个更长的LIS，因为当前状态下最长序列的结尾元素是6 我们找到第一个大于5的位置，也就是6所在的位置做替换。这是因为5可以接续在元素4，同样得到一个长度为 5 的序列，而对于两个长度为5的上升子序列

• [.... ] 6
• [.... ] 5

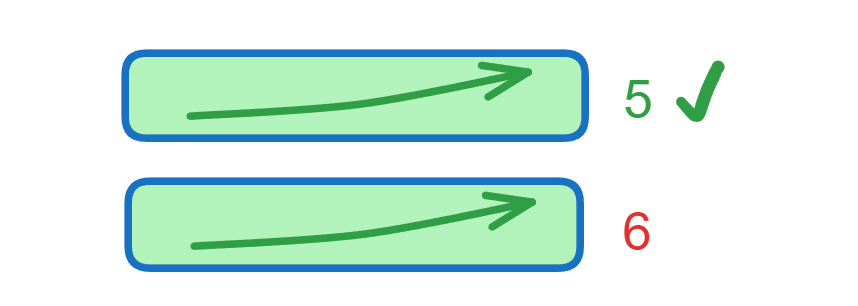
根据之前的原则，我们保留结尾元素小的。故更新q[5] 为 5。

注意

在查找第一个大于新元素的序列尾部时，可以使用二分查找来提高效率，因为队列是单调的。

答案

问题的答案即是最后这个单调队列内的有效元素的数量。

完整代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;

// q是一个单调队列 记录了序列长度和该尾部对应的结尾元素
// 对于长度相同的序列 选择更小的的结尾元素 因为它有更好的可扩展性
int a[N] , q[N];

int main()
{
    int n ; cin >> n;
    for (int i = 1; i <= n; i ++ )
        scanf("%d", &a[i]);

    int len = 0;
    for(int i = 1 ; i <= n ; i++)
    {
        // 利用二分查找 找到最后一个小于该目标元素(a[i])
        // 即找最后一个可接的元素
        int l = 0 , r = len;
        while(l < r)
        {
            int mid = (l + r + 1) / 2;
            if(q[mid] < a[i]) l = mid;
            else r = mid - 1;
        }
        // 如果可接元素为最后一个 那么需要将(最长子序列)长度扩展一位
        if(l == len) len++;
        q[r+1] = a[i]; // 设置目标长度的结尾位置
    }

    cout << len;
}

双串阶段划分

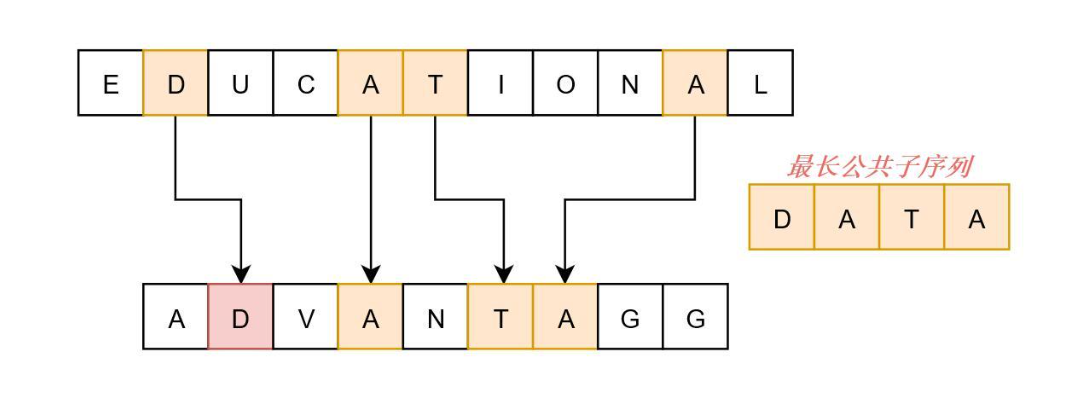
最长公共子序列

状态表示

输入串A，串B。f是二维数组，长宽对应串A和串B的长度。f[i][j]表示串A的前i个元素和串B的前j个元素对应的 LCS 长度。

递推

在计算一个新的位置时，分两种情况讨论。第一种A[i] == B[j]

此时 f[i][j] = f[i-1][j-1] + 1。即我们直接讲 A[i] , B[j]放入 LCS 中，并且将它们前部分的 LCS 答案加上 1。因为这两个元素在当前子问题的末尾，所以这样做一定会得到一个最优的答案。或者说这个问题的解具有单调性，f[i-1][j-1]是所有可能的转移里最大的那个。

当A[i] != B[j] 时，思考所有就近的转移。包括f[i-1][j] , f[i][j-1] , f[i-1][j-1]因为此时无法拓展 LCS 的长度，所以取先前答案的最大着作为当前问题的答案。

事实上 f[i-1][j-1]一定小于等于另外两者，因为它是另外两者的一个子问题。所以只需要另两个状态的最大值即可。

完整代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;
char a[N] , b[N];
int f[N][N];

int main()
{
    int n , m;
    cin >> n >> m;

    scanf("%s" , a+1);
    scanf("%s" , b+1);

    // f[i][j] a的前i个字符和b的前j个字符的公共子序列长度
    for(int i = 1 ; i <= n ; i++)
    {
        for(int j = 1 ; j <= m ; j++)
        {
            f[i][j] = max(f[i-1][j] , f[i][j-1]);
            if(a[i] == b[j])
            {
                f[i][j] = max(f[i][j] , f[i-1][j-1] + 1);
            }
        }
    }
    cout << f[n][m];
}

编辑距离

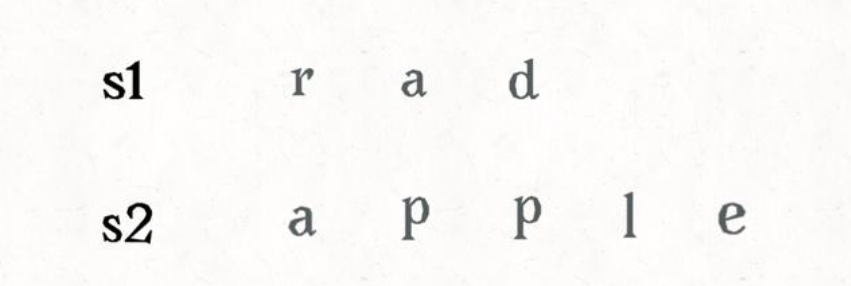
状态表示

二维数组，f[i][j]表示 s1的前i个字符和s2的前j个字符的编辑距离。

递推

这个问题和 LCS 问题有相似之处。当s1[i] == s2[j]时，这两个字符间不存在编辑距离，所以此时f[i][j] = f[i-1][j-1]。

否则，在f[i-1][j] , f[i][j-1] , f[i-1][j-1]这三种情况中取最小者再 加 1。

f[i][j] = min(f[i-1][j-1] , f[i-1][j] , f[i][j-1]) + 1;

我们可以选择讲这两个元素变为相同，或者去掉其中一个元素。则这对应了三种情况。

第二点需要解释的是，为什么此时f[i-1][j-1]不是f[i][j-1]或f[i-1][j]的子问题，我们举反例说明。

例子 1

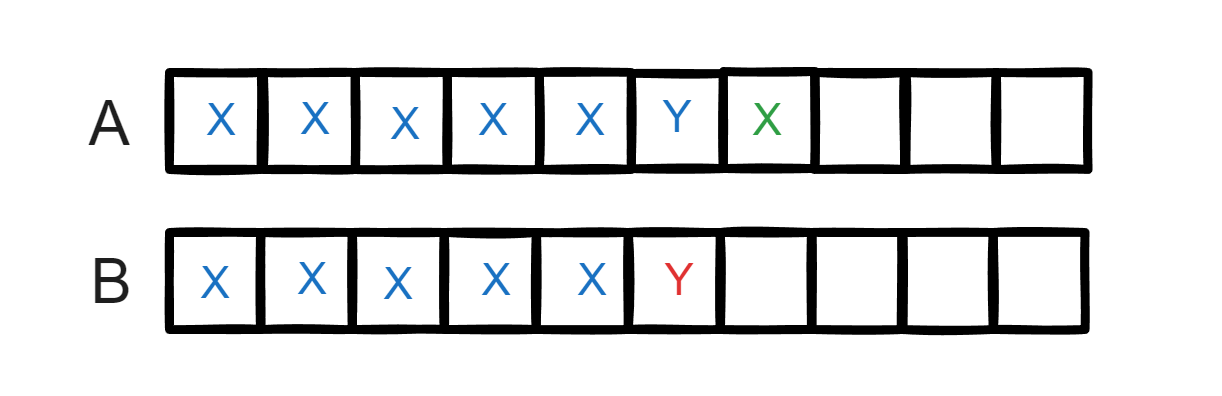
这种情况下直接去掉 s[i] 即 X 更好 , 因为虽然 s1[i] != s2[j] 但是直接删掉X后，两者的前半部分是完全一样的。

例子 2

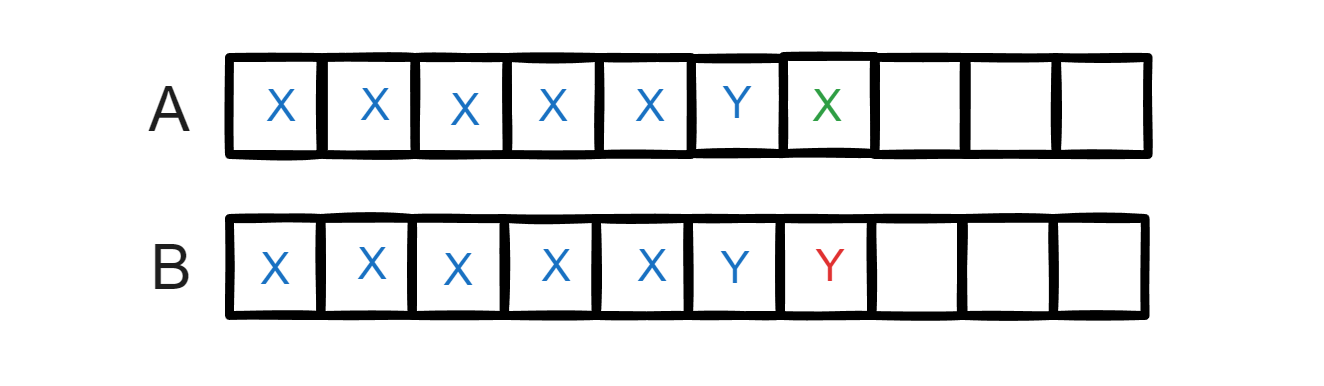
显然此时直接将s1[i]变为 s2[j]编辑距离更短。这时的转移是 f[i-1][j-1] + 1

初始化

因为任何空串到其他串的编辑距离都为这个目标串的长度，所以需要对 f[i][0]和f[0][i]所表示的这一列和这一行做初始化。

完整代码

#include <bits/stdc++.h>
using namespace std;

const int N = 2010;
char a[N] , b[N];
int f[N][N];

int main()
{
    int n , m;
    cin >> n >> m;
    scanf("%s" , a+1);
    scanf("%s" , b+1);

    for(int i = 0 ; i < N ; i++)
    {
        f[i][0] = i;
        f[0][i] = i;
    }


    for(int i = 1 ; i <= n ; i++)
        for(int j = 1 ; j <= m ; j++)
            if(a[i] == b[j])
	            f[i][j] = f[i-1][j-1];
            else
	            f[i][j] = min(f[i-1][j-1] , min(f[i][j-1] , f[i-1][j])) + 1;

    cout << f[n][m];
}

二维输入

数字三角形

存储和状态表示

将数字三角形存储在矩阵的下三角区域。

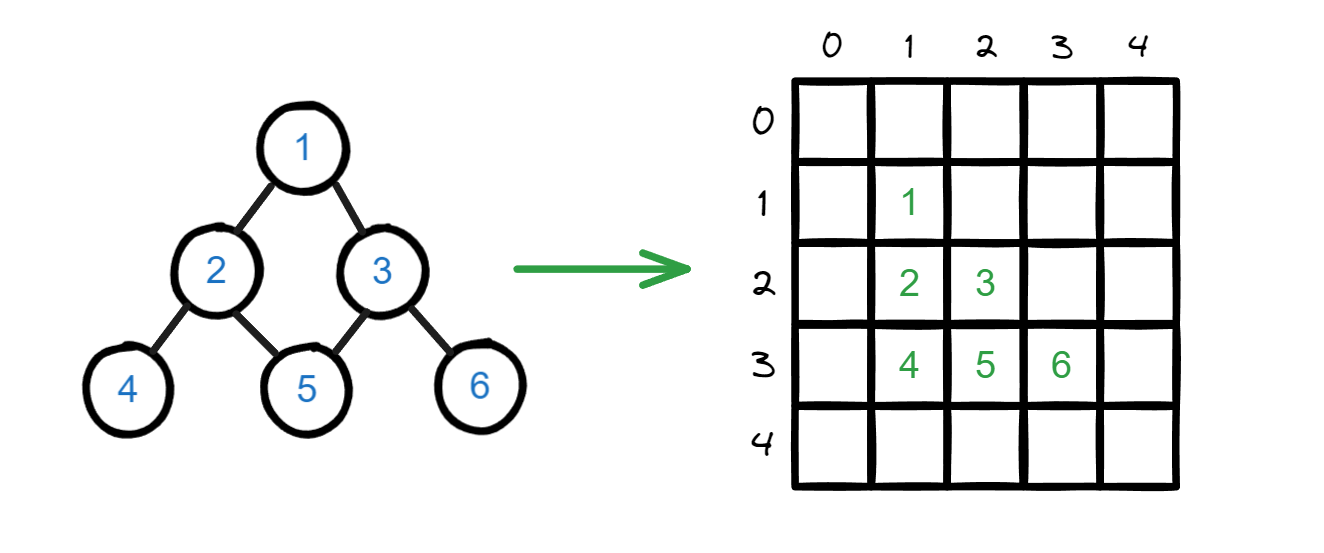
和存储矩阵同大小的状态矩阵，f[i][j]表示到达存储矩阵对应位置可以的得到的数字之和最大值。

递推

在本问题中，可以直接将原问题存储在f中。对于每个位置，可能从该位置的左上方和右上方到达，选择其中累计更大的那个作为转移。

f[i][j] += max(f[i-1][j] , f[i-1][j-1]);

边界

这里的边界指在原来的三角形中不存在的位置，例如f[2][1] = max(f[1][1] , f[1][0]),但f[1][0]不是一个合法的位置，要避免这些转移，将边界设置为负无穷。

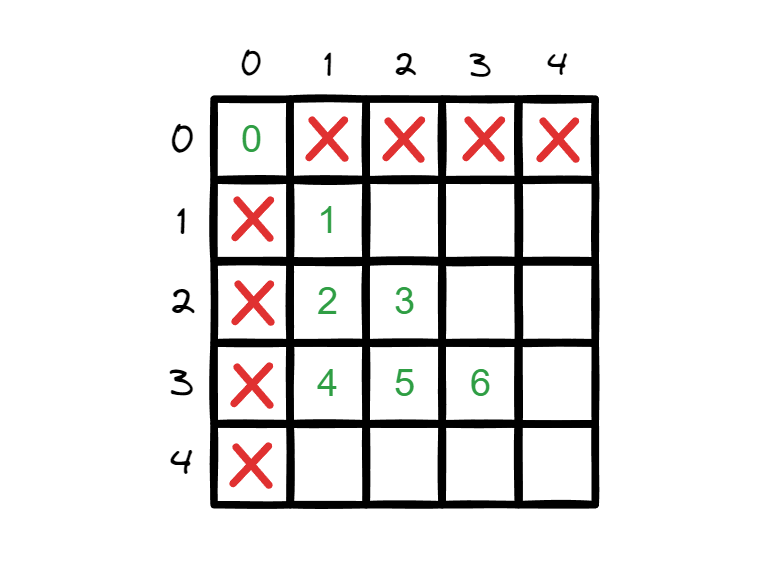
答案

根据题意，答案为f最后一行的最大值。

完整代码

#include<iostream>
#include<cstring>
using namespace std;

const int N = 510 , INF = 1e9;
int f[N][N];

int main()
{
    for(int i = 0 ; i < N ; i++)
        for(int j = 0 ; j < N ; j++)
            f[i][j] = -INF;

    f[0][0] = 0;

    int n; cin >> n;
    for(int i = 1 ; i <= n ; i++)
    {
        for(int j = 1 ; j <= i ; j++)
        {
            cin >> f[i][j];
            f[i][j] += max(f[i-1][j-1] , f[i-1][j]);
        }
    }

    int res = -INF;
    for(int i = 1 ; i <= n ; i++) res = max(res , f[n][i]);

    cout << res;
}

试一试

• 打家劫舍
• LIS1
• LIS2
• LCS
• 编辑距离
• 数字三角形