讲解了树状数组的概念，理解和使用场景。

概述

树状数组（Fenwick Tree），又叫二进制索引树（Binary Indexed Tree, BIT），是一种支持动态数组中区间求和(O(lgN))和单点修改(O(lgn))操作的数据结构。它在时间复杂度和空间复杂度上都具有较好的表现，尤其适合于解决一些需要频繁更新和查询的数据问题。

其主要思想是维护一颗关联树，树的每个节点代表了原数组种某一段的信息，这棵树可以存储在数组里。

图解

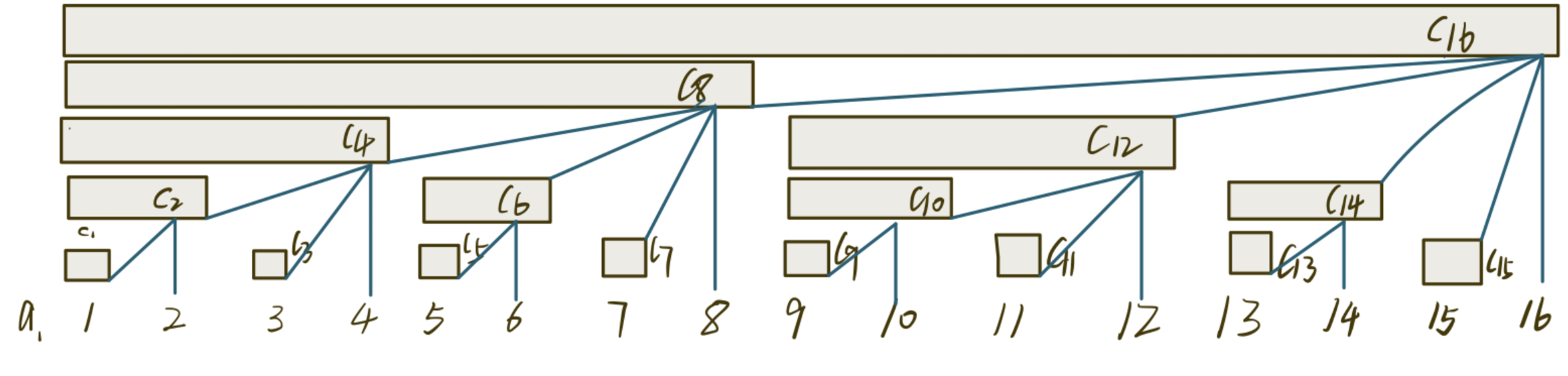
可以这样思考这个问题，就像在玩消消乐或者2048游戏一样，每两个 1️⃣ 区间会合成为 一个 2️⃣ 区间，每两个 2️⃣ 区间会合成为一个 4️⃣ 区间 这种合成是自动发生的。所以从数组的末尾位置往前看，最上层每种长度的区间只会有一个。

lowbit

lowbit(x)返回 x的二进制表示中最低位的 1 表示的值。

例如 lowbit(1100) = 0b(100) = 4

int lowbit(int x)
{
	return x & -x;
}

定点更新

定点更新原数组某个位置，需要递归向上更新其所有父辈节点。

例如，需要更新 5 时，需要同时 更新 c5 c6 c8 c16这些位置，我们来一探其中的规律。

5 = 0b(101), 最低位的 1代表其为叶子节点。其直接父亲为 5 + lowbit(5) = 6

6 = 0b(110), 最低位的 1代表其为倒数第二层的中间节点。其直接父亲为 6 + lowbit(6) = 8

8 = 0b(1000), 最低位的 1代表其为倒数第三层的中间节点。其直接父亲为 8 + lowbit(8) = 16 可以用一个循环写出更新路径

int x;
for(int i = x ; i <= n ; i += lowbit(i)) update(i);

区间查询

查询起点到某个点的和。需要利用查询点左侧已经归档的块。

例如要查询 [1 - 14] , 看图可知为 c8 + c12 + c14。问题可以理解，当前已经合成的区间有那些？自然，对于当前已经合成区间，其在二进制位上的表现为 1。

• 14 = 0b(1110)
• 12 = 0b(1100)
• 8 = 0b(1000)

故可以写出

long long sum(int x)
{
	long long res = 0;
	for(int i = x ; i ; i -= lowbit(i)) res += fenwick[i];
	return res;
}

例题

Acwing 242

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;

int n , m;
int a[N];
LL tr[N]; // Fenwick 关联数组 将原数组提取为一棵树

// lowbit 最低位1所标志的整数
int lowbit(int x)
{
    return x & -x;
}


void add(int x , int c)
{
    for (int i = x ; i <= n ; i += lowbit(i)) tr[i] += c;
}

LL sum(int x)
{
    LL res = 0;
    for (int i = x ; i ; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n ; i ++) scanf("%d" , &a[i]);
    
    // 将输入数组视为某个前缀和数组 那么通过差分的方式可以求出原数组
    // 求出原数组的每个位置之后 
    for (int i = 1 ; i <= n ; i ++) add(i , a[i] - a[i-1]);
    
    while(m --)
    {
        char op;
        int l , r , d;
        int x;
        cin >> op;
        
        if (op == 'C')
        {
            scanf("%d%d%d", &l , &r , &d);
            // 在差分数组上修改两个点,相当于在原数组的端点上操作
            add(l , d) , add(r + 1 , -d);
        }
        else
        {
            scanf("%d" , &x); // 第x数的值,由差分数组的前n个数求和得到
            printf("%lld\n" , sum(x));
        }
    }
    
    return 0;
}