KMP
讲述了用于优化字符匹配的kmp算法的思想和编码实现。
什么是 KMP 算法？
KMP 算法由 Donald Knuth、Vaughan Pratt 和 James H. Morris 于 1977 年共同提出。它用于在主串（文本）中高效地查找模式串（子字符串）的所有出现位置。与朴素的字符串匹配算法不同，KMP 能够在发生部分匹配失败时，通过预处理模式串的信息，避免不必要的重复比较，从而实现线性时间复杂度。
KMP 算法的基本原理
KMP 算法的核心思想是利用模式串本身的信息，避免在匹配过程中回溯主串的指针。具体来说，KMP 在匹配过程中，当出现不匹配时，根据已经匹配的部分，跳过主串中不可能匹配的位置，直接移动模式串的位置，从而减少比较次数。
为了实现这一点，需要知道模式串任意前缀的最长公共前后缀长度。KMP 算法预处理模式串，构建一个部分匹配表，用于在匹配失败时指导模式串的移动。
部分匹配表
部分匹配表是一个数组，用于记录模式串中每个位置之前的子串的最长相等的前缀和后缀的长度。具体来说，对于模式串的每一个位置 i，部分匹配表 lps[i] 表示子串 pattern[0...i-1] 的最长相等前缀和后缀的长度。
例如，考虑模式串 ABABC：
- 对于
A，没有前缀和后缀，lps[0] = 0 - 对于
AB，前缀A和后缀B不同，lps[1] = 0 - 对于
ABA，前缀A和后缀A相同，lps[2] = 1 - 对于
ABAB，前缀AB和后缀AB相同，lps[3] = 2 - 对于
ABABC，前缀ABAB和后缀BABC没有相同的前缀和后缀，lps[4] = 0
因此，部分匹配表为 [0, 0, 1, 2, 0]。
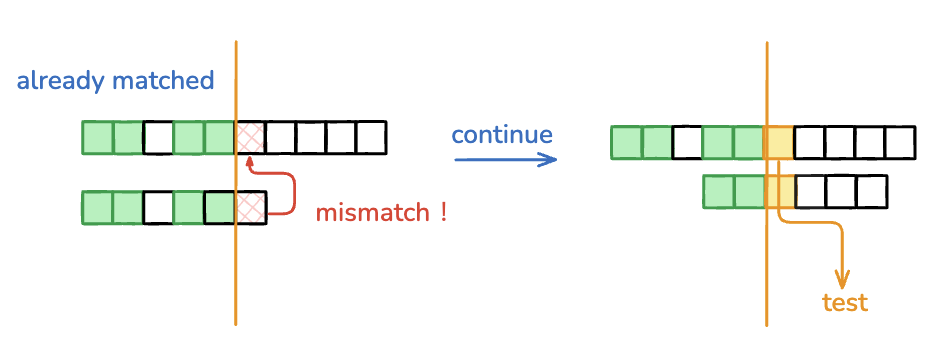
情况1
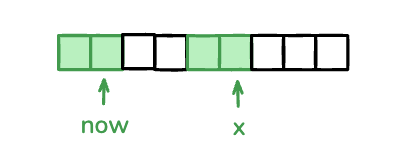
now == x时，两个指针各延伸一位，并且记录公共前后缀的长度。
情况2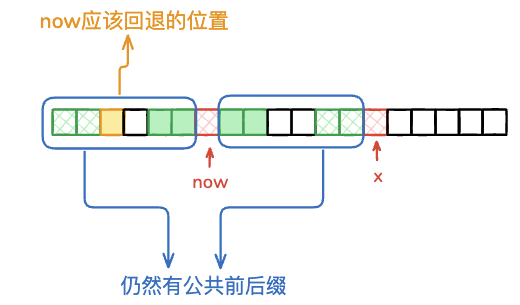
匹配
使用两个工作指针进行匹配，有四种情况。
情况一 - 未完全匹配
模式串和字符串中的工作指针指向的字符相同，但是没有完全匹配模式串。
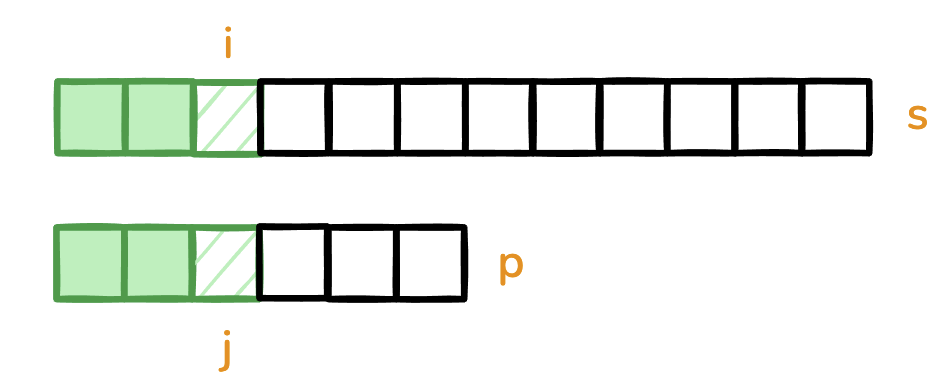
将两个工作指针同时向后移动一位。
情况二 - 匹配成功
完成模式串的匹配。
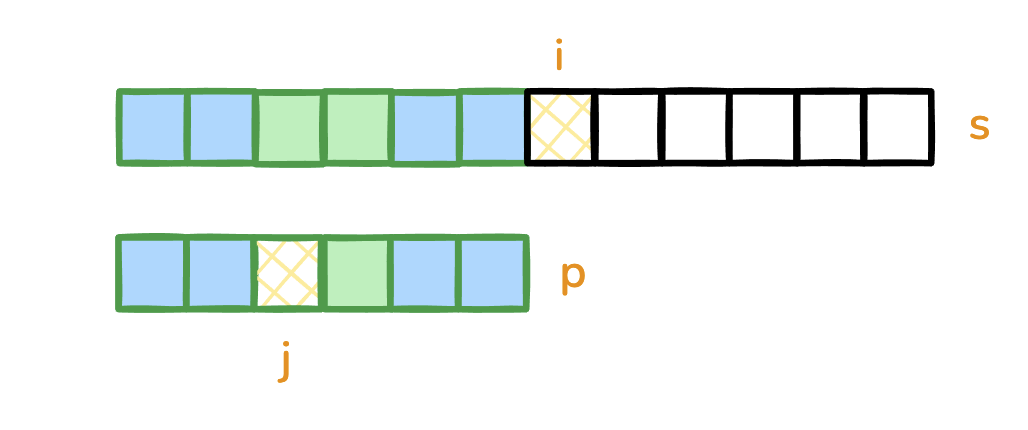
将 字符串中的指针移动一位，模式串中按照匹配成功的当前位置的字串(即整个串)的next数组进行回退 , j = next[j]。
情况三 - 部分失配
发生失配，但是模式串的工作指针不为 0。
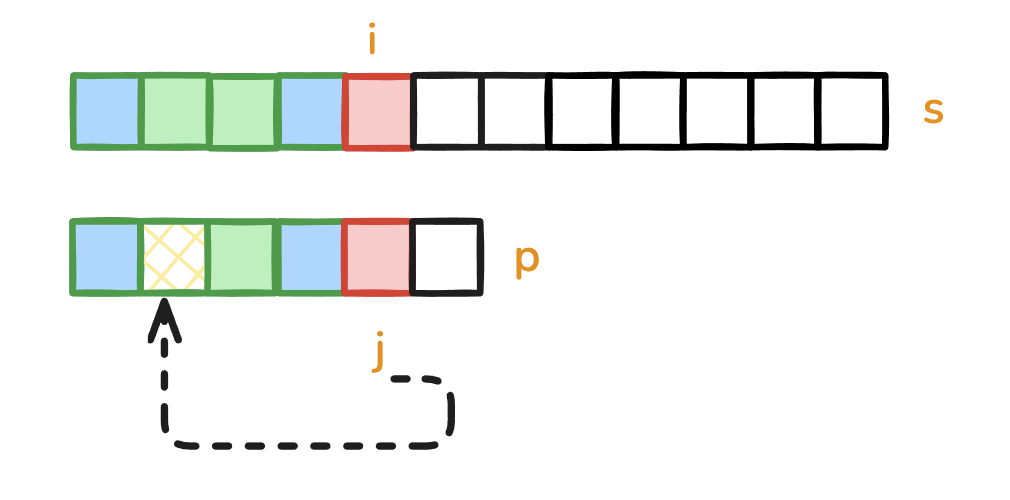按照已经匹配部分的next数组进行回退, j = next[j - 1]。
情况四 - 完全失配
模式串已经回退到头部， 但仍然失配。
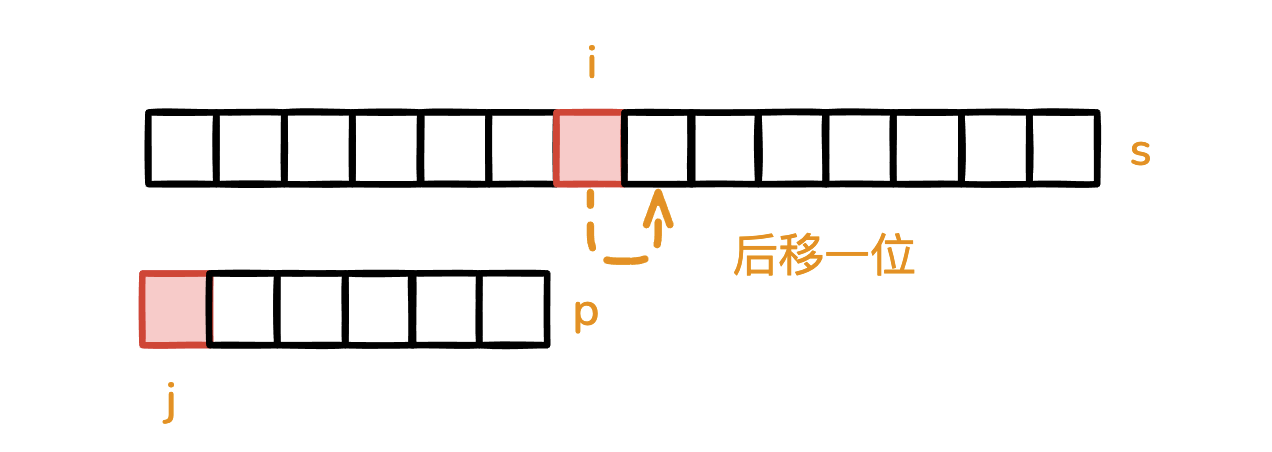
字符串的指针向后移动一位。
编码实现
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int next[N];
char s[N] , p[N];
void build_next(int n)
{
// 初始化两个指针 拥有相同公共前后缀的串长度至少为2
int now = 0 , x = 1;
while(x < n)
{
// 尝试延长最长公共前后缀的长度
if(p[now] == p[x])
{
// next 数组
now++;
next[x] = now; // 记录此时的公共前后缀长度 也是失配发生是模式串回退的位置
x += 1;
}
else if(now)
{
// 失匹 但now不为零 那么试图回退now 看看是否能与x所在位置匹配
// 回退的原则是 在已构造的pm中找0 ~ now的匹配前后缀 因为0 ~ now-1的匹配前后缀和 ~ x-1 的是完全一样的 所以如 p[pm[now-1]]
now = next[now - 1];
}
else // now == 0
{
pm[x++] = 0; // 完全失配
}
}
}
// n 是模式串长度
// m 是字符串长度
void match(int n , int m)
{
int i = 0 , j = 0;
while(i < m)
{
if(p[j] == s[i])
{
// 匹配到模式串的最后一位
if(j == n - 1)
{
// 输出在字符串中的起点
cout << i - n + 1 << " ";
// 按next数组回退以期继续匹配
j = next[j];
i = i + 1;
continue;
}
i ++ ; j ++;
}
else if(j)
{
j = next[j - 1];
}
else
{
i ++ ;
}
}
}
int main()
{
int n , m ;
cin >> n >> p >> m >> s;
build_next(n);
match(n , m);
}版权所有
版权归属：