ST Table
讲解了st表使用场景和构造方法。
RMQ问题
在计算机科学与算法设计中，区间最小值查询（Range Minimum Query，简称 RMQ） 是一个经典且广泛应用的问题。RMQ 的目标是在一个数组中，快速找到指定区间内的最值。
ST表
稀疏表是一种用于静态数组的预处理数据结构，能够在常数时间内回答区间查询问题。它特别适用于不可变数组的情况，即数组在预处理后不再发生变化。
ST 表基于动态规划的思想，通过预处理不同长度的区间信息，来快速回答RMQ查询。 ST 表通过倍增区间的方法处理区间，使得 DP表的空间占用为 O(nlgn), n为区间长度。
倍增区间
求出区间长度范围内，所有以2^k k=1,2,3..为长度的区间的最值。
dp[i][k] 代表以i为起点，2^k为区间长度的最值。
以最小值为例，可以这样推导
dp[i][k] = min(dp[i][k-1] , dp[i + (1 << (k-1))][k-1]) 即两边由两边区间的最小值推得。
处理查询
query(i , j)可以从起点i开始找两个长度为2^k重叠得到
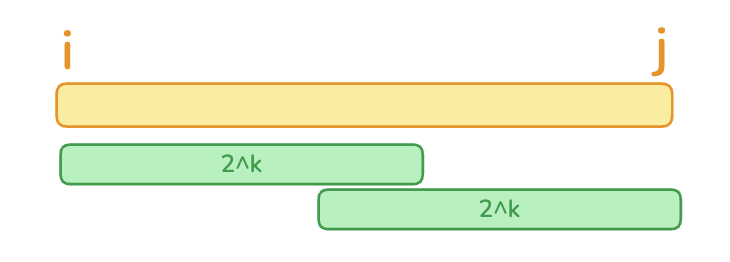
query(i , j) = min(dp[i][k] , dp[j-(2 << k) + 1][j]) 其中 k = floor(lg2(j - i + 1))。
编码实现
#include<iostream>
#include<cmath>
using namespace std;
int n , m;
const int N = 2e5 + 10, M = 20;
int f[N][M];
void build_st()
{
int t = log2(n);
// f[i][k] 表示以 i 开头的 长度为 2^k 区间的最值
// f[i][k] 的起点是 i , 终点是 i + 2^k -1
for (int k = 1 ; k <= t ; k ++)
{
for (int i = 1 ; i + (1 << k) - 1 <= n ; i++)
{
// 该区间的最值 由其两边区间的最值转移
f[i][k] = max(f[i][k-1] , f[i + (1 << (k-1))][k - 1]);
}
}
}
int query(int l , int r)
{
int k = log2(r - l + 1); // 赋值时已经向下取证了
return max( f[l][k] , f[r - (1 << k) + 1][k]);
}
int main()
{
cin >> n;
for(int i = 1 ; i <= n ; i++)
cin >> f[i][0];
build_st();
cin >> m;
while(m --)
{
int l , r ; cin >> l >> r;
cout << query(l , r) << endl;
}
}版权所有
版权归属：