Algorithm›Graph

Construction of Graph

About 682 wordsAbout 2 min

图论

2024-7-6

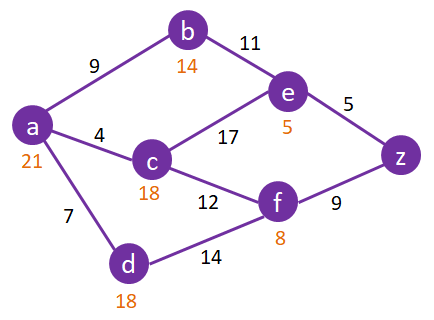cover
本篇文章讲述的图的构建方式

概述

本文从解决算法问题的角度，给出几种图的构建方式，他们的代码实现，特点以及优缺点分析。这些构建方式分别是:

邻接矩阵 - 二维数组
邻接表 - 向量表
邻接表 - 哈希表
邻接表 - 模拟数组

邻接矩阵 - 二维数组

代码实现

#include<cstring>
using namespace std;

const int N = 1e3;
int graph[N][N];

void init()
{
	memset(graph , 0x3f , sizeof graph);
}

void add(int a , int b , int c)
{
	graph[a][b] = min(graph[a][b] , c);
}

特点

实现简单。
可以在O(1)复杂度实现边的存在性判断和去重。
在内存限制为256MB的情况下，最多可以开出数量级为1e3。
对于稀疏图的存储效率不高。

适用场景

小规模稠密图
小规模图

邻接表 - 向量表

代码实现

#include<vector>
#include<utility>
using namespace std;

typedef pair<int , int> edge;
const int N = 1e5;
vector<edge> graph[N];

void init()
{
	return;
}

void add(int a , int b , int c)
{
	graph[a].push_back({b , c});
}

特点

使用向量代替链表，逻辑简单。
无法在O(1)复杂度内判别边，也无法在O(1)复杂度内去重。
向量结构的维护带来额外的时间成本。

适用场景

中等及以下规模图。

邻接表 - 哈希表

代码实现

#include<unordered_map>
using namespace std;

const int N = 1e5;
unordered_map<int , int> graph[N];

void init()
{
	return;
}

void add(int a , int b , int c)
{
	if(graph[a].count(b) > 0)
	{
		graph[a][b] = min(graph[a][b] , c);
	}
	else
		graph[a][b] = c;
}

特点

用哈希表替代了链表。
可以用O(1)复杂度实现判别边和去重。
建图需要维护哈希表所带来的额外时间和空间代价。

使用场景

大规模稀疏图
频繁查询的场景

邻接表 - 模拟数组

代码实现

#include<cstring>
using namespace std;

const int N = 1e5 , M = 3e5;
int h[N] , e[M] , ne[M] , w[M] , idx;

void init()
{
	memset(h , -1 , sizeof h);
}

void add(int a , int b , int c)
{
	e[idx] = b; w[idx] = c; ne[idx] = h[a]; h[a] = idx++;
}

特点

模拟数组带来了极致的存储效率，建图过程快速。
无法在O(1)复杂度内完成边的判别和去重。

适用场景

大规模图
频繁建图

总结

建图方式\特点	建图速度	0(1)判边	0(1)去重	图规模	图特点
邻接矩阵 - 二维数组	快	是	是	小	稠密
邻接表 - 向量表	中	否	否	中	稀疏
邻接表 - 哈希表	中	是	是	中大	一般
邻接表 - 模拟数组	快	否	否	中大	稀疏