历史

在 18 世纪初，普鲁士的哥尼斯堡（今日俄罗斯的加里宁格勒）被普列戈利亚河分成了南北两岸，河中心还有两座岛屿。岛屿与河的两岸由七座桥连接，如下图所示。

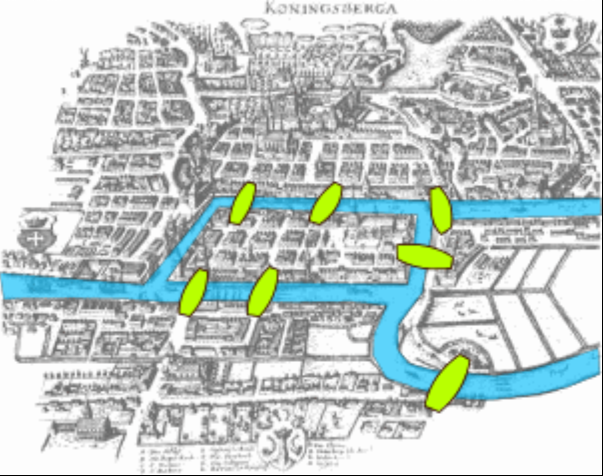
当时，当地居民在桥上散步的过程中，逐渐产生了一项有趣的消遣活动：找到一条从任意地点出发的路径，经过每座桥恰好一次，并回到出发点。

这个谜题看似简单，然而许多年过去了，都没有人找到符合要求的路径。1735 年，时年 28 岁的数学家欧拉也听说了这一问题。经过了一段时间的研究后，欧拉对该问题做出了分析。欧拉对哥尼斯堡七桥问题的分析更加抽象化。首先，欧拉将每片地区抽象为一个点，并将每座桥抽象为连接两点的一条线，得到如下抽象图形。同学们看这张图一定会觉得非常熟悉，事实上，欧拉对哥尼斯堡七桥问题的研究正是图论的开端。

定义

• 欧拉路径：指的是一条经过图中每一条边恰好一次的路径，但不要求必须回到起点。
• 欧拉回路：是指一条经过图中每一条边一次且仅一次，并且最终回到起点的路径。欧拉回路是欧拉路径的特殊情况。
• 欧拉图：存在欧拉回路的图称作欧拉图。
• 半欧拉图：存在欧拉路径但不存在欧拉回路的图称作半欧拉图。

存在条件

前提: 所有边都是联通的。

无向图

• 欧拉回路的充分必要存在条件：如果图中所有顶点的度数都是偶数，则存在欧拉回路。
• 欧拉路径的充分必要存在条件：如果图中恰好有两个奇度顶点，则存在欧拉路径，但路径的起点和终点必须是这两个奇度顶点。

有向图

• 欧拉回路的充分必要条件：所有顶点的出度和入度都相等。
• 欧拉路径的充分必要条件: 恰好有一个顶点的出度比入度大1，且恰好有一个顶点的入度比出度大1，其余所有顶点的入度和出度相等。

希尔霍尔策算法

基本思想是首先找到一个子回路，并逐步将其他回路合并到该子回路中，最终形成完整的欧拉回路。该证明被后人整理成 Hierholzer 算法，用于在已经判定无向图的欧拉回路存在的前提下，找出一条欧拉回路。算法流程如下：

• 寻找子回路：从任意非零度节点 u 出发，沿着边遍历图。在遍历过程中，删除经过的边。如果遇到一个所有边都被删除的节点，那么该节点必然是 u，即我们找到了一个包含 u 的回路。将该回路上的节点和边添加到结果序列中。

• 检查是否存在其它回路：检查刚刚添加到结果序列中的节点，看是否还有与节点相连，且未遍历的边。如果发现节点 u 有未遍历的边，则从 u 出发重复步骤 1，找到一个包含 u 的新回路，将结果序列中的一个 u 用这个新回路替换。此时结果序列仍然是一个回路，只不过变得更长了。

• 结束条件：重复步骤 2，直到所有边都被遍历。此时结果序列中的节点和边就构成了欧拉回路。算法结束。

求解回路

使用深度优先搜索，在函数退栈时保存路径。保存的路径的顺讯和搜索顺讯相反。

对于欧拉回路，从任一节点出发即可；对于欧拉路径，从路径起点开始搜索，搜索会在路径终点结束，然后回溯进行回路添加。

图解

对于图示的结构，一次可能的搜索路径为

• 1 -> 2 -> 3 -> 4 回溯至2
• 1 -> (2 -> 5 -> 6 -> 7) -> 3 -> 4 (完整欧拉路径)

代码实现

根据 Acwing 模板题1184进行的综合实现代码

#include<bits/stdc++.h>
using namespace std;

const int N = 1e5+10 , M = 4e5+10;

/*
    对于有向图 m 条边 会存储在 0 - m-1 这些 下标位置
    对于无向图 2m 条边 会存储在 0 - 2m-1 这些 下表位置
    
    对向边 存储在 诸如 (0 , 1) : 1 , (2 , 3) : 2  , (4 ,5) : 3 这些位置
*/
int h[N] , e[M] , ne[M] , idx;
int din[N] , dout[N];
int ans[M] , cnt;
int use[M];
int type;

void init()
{
    memset(h , -1 , sizeof h);
}

void add(int a , int b)
{
    e[idx] = b ; ne[idx] = h[a] ; h[a] = idx ++;
}

void dfs(int u)
{
	// 使用引用直接改变邻接表表头 达到删除边的目的
    for(int& i = h[u] ; i != -1 ; )
    {
        if(use[i])
        {
            i = ne[i];
            continue;
        }
        
        use[i] = true;
        if(type == 1) use[i ^ 1] = true;

		// 将边的存储下表和自然下标做换算
        int t;
        if(type == 1)
        {
            t = i / 2 + 1;
            if(i % 2 == 1) t = -t;
        }
        else t = i + 1;
        
        int j = e[i];
        i = ne[i];
        
        dfs(j);

		// 在退栈时记录路径上的边(或可选记录节点)
        ans[ ++ cnt ] = t;
    }
}


int main()
{
    init();
    
   cin >> type;
   int n , m; cin >> n >> m;
   
   for(int i = 0 ; i < m ; i++)
   {
       int a , b; scanf("%d %d" , &a , &b);
       add(a , b);
       if(type == 1) add(b , a);
       
       din[b] ++ ; dout[a] ++;
   }


	// 判别无向图中欧拉回路存在的条件
   if(type == 1)
   {
       for(int i = 1 ; i <= n ; i ++)
       {
           if( (din[i] + dout[i]) % 2 == 1)
           {
               cout << "NO";
               return 0;
           }
       }
   }
   else // 判别有向图中欧拉回路存在的条件
   {
       for(int i = 1 ; i <= n ; i++)
       {
           if(din[i] != dout[i])
           {
               cout << "NO";
               return 0;
           }
       }
   }
   
   // 找到一个有出边的节点 进行遍历
   for(int i = 1 ; i <= n ; i++)
   {
       if(h[i] != -1)
       {
           dfs(i);
           break;
       }
   }

	// 一次遍历应该包含所有的边
   if(cnt != m)
   {
       cout << "NO";
       return 0;
   }
   
   cout << "YES" << endl;
   for(int i = m ; i >= 1 ; i--) cout << ans[i] << " ";
}