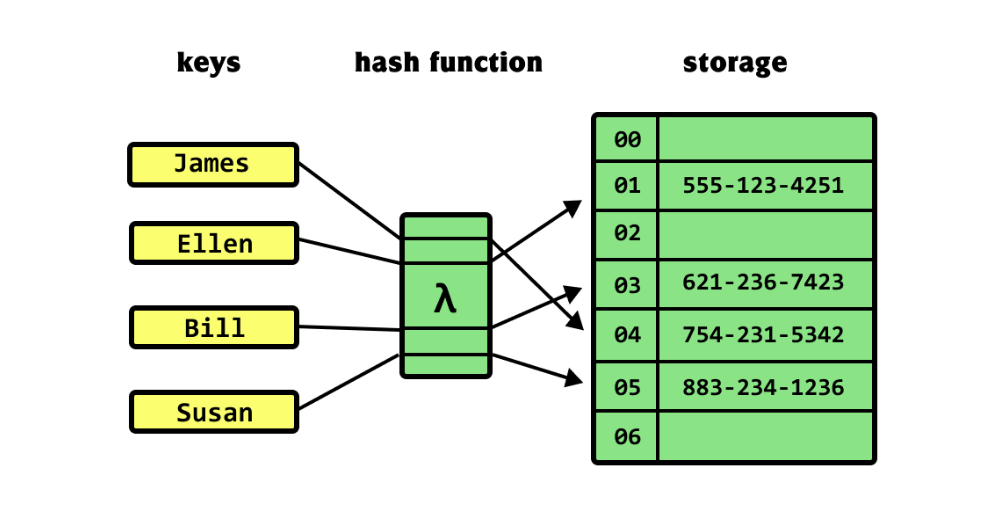
Concept of Hashing
文章参考了enjoy algorithms的相关内容
为什么需要哈希表
许多应用程序（例如翻译编程语言的编译器）需要有效的机制来支持插入、搜索和删除等字典操作。例如，编译器可以维护一个符号表，其中元素的键是与语言中的标识符相对应的字符串。为了支持编译器所需的各种操作，符号表需要高效。
使用数组或链表实现符号表或字典操作的一个问题是搜索元素所需的时间。例如，如果数据存储在数组中，则搜索元素所需的时间将为 O(log n) 或 O(n)，具体取决于数组是否已排序。在我们需要处理大型数据集的情况下，由于搜索所需的时间，O(n) 场景可能不是一个可行的选择。
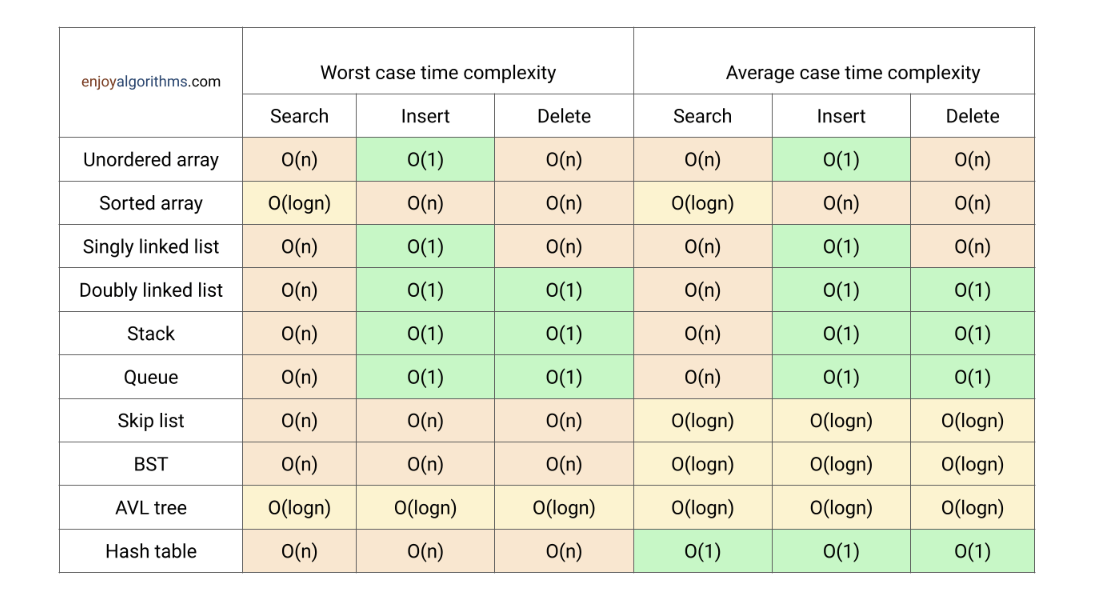
另一方面，在哈希表中搜索元素通常平均需要 O(1) 时间，最坏情况下的时间为 O(n)。虽然在最坏的情况下散列可能需要 O(n) 时间，但它通常平均表现得非常好。因此，了解哈希的概念以及哈希表和哈希函数等相关概念非常重要。
直接地址表(Direct Address Table)
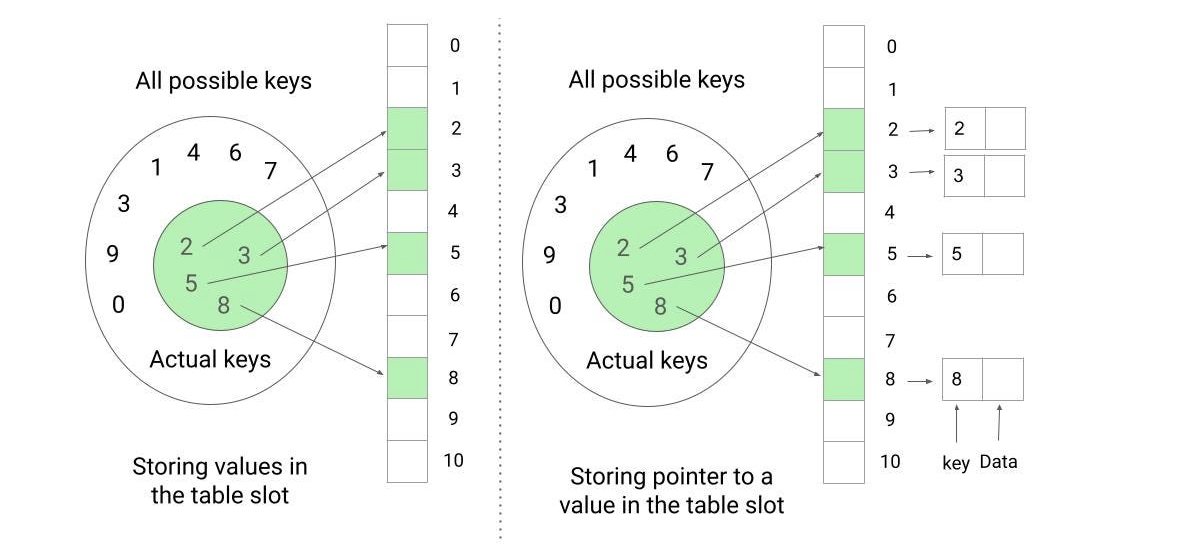
如果应用程序需要一个数据存储机制，其中每个元素都有一个小键，并且键是从 0 到 m - 1 的不同整数，我们可以使用数组 T[0..m-1] 来存储元素。具有键 k 的元素被放置在 T[k] 处，如果不存在具有键 i 的元素，则 T[i] 被设置为 NIL。根据应用程序，我们可以将值本身存储在 T[k] 中，也可以仅存储指向该值的指针。
这种方法允许我们使用元素的键轻松访问元素，因为我们可以在数组中相应的索引处查找元素。换句话说，直接地址表的思想允许在 O(1) 时间内执行插入、搜索和删除等字典操作。然而，如果键的范围很大，它可能不是最有效的解决方案。
挑战
使用直接地址表时需要考虑几个关键点：
- 提前了解秘钥的上限
- 键在比较小的范围时，直接地址表比较有效
- 如果实际的键数与可能的键总数相比较小，则直接地址表可能会导致内存空间的浪费。这是因为该表需要一个数组，其中每个可能的键都有一个槽。
总之，当键是小范围内的整数时，直接地址表是一种有用的数据结构，并且我们可以为每个可能的键分配一个具有一个槽的数组。如果键不是整数或者范围很大，我们需要一个高效的数据结构来执行字典操作。
哈希表
哈希表是一种数据结构，允许使用任何数据类型的键有效存储和检索元素。当实际键数与可能键总数相比较小时，它是直接地址表的一个很好的替代方案。
h(k)，用于根据键 k 计算数组索引或“槽”。然后，具有键 k 的元素将存储在哈希表中的该槽中。哈希函数使哈希表能够使用任何数据类型的键来存储和访问元素，而不是局限于小范围内的整数键。
哈希表比直接地址表需要更少的存储空间，因为它使用大小与实际键数量成比例的数组，而不是为每个可能的键分配一个槽。这使我们能够将存储要求减少到 O(m)（其中 m 是实际键的总数），同时仍然保持 O(1) 平均搜索时间的优势。
散列涉及三个主要步骤:
- 预处理输入数据以计算密钥（整数）。密钥本身不必是整数，而是可以从输入数据中的相关信息导出。
- 使用哈希函数将键转换为数组索引。
- 使用哈希函数生成的索引来插入、删除或访问哈希表中所需的值。
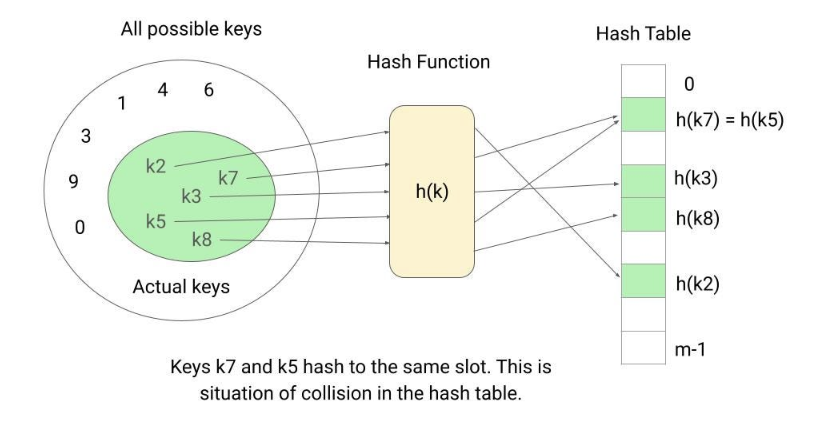
碰撞 (collision)
散列的一个潜在问题是两个密钥可以散列到同一个槽，这称为冲突。虽然完全避免碰撞是理想的选择，但这实际上是不可能的。因此，有必要制定冲突发生时的解决方案。
减少冲突次数的一种方法是选择设计良好的“看起来随机”的哈希函数。然而，即使使用良好的哈希函数，冲突仍然可能发生。在这种情况下，我们需要一种解决冲突的方法。冲突解决有两种主要方法： 拉链法 和 开放寻址法。
时空权衡(T-M tradeoff)
散列是一种允许我们在使用键搜索元素时平衡时间和内存之间的技术。在没有内存限制的理想情况下，我们可以通过简单地使用键作为大型数组中的索引，仅使用一次内存访问来搜索元素。然而，当可能的键总数远大于实际键数时，这是不切实际的，因为它需要过多的内存。
另一方面，如果没有时间限制，我们可以在无序数组中使用线性搜索，但当元素数量变大时，效率会很低。
哈希提供了一种平衡这两个极端的方法，允许我们调整参数以在时间和内存之间进行权衡。这是无需重写代码即可实现的，使其成为使用键搜索元素的灵活且高效的技术。
均匀散列
在散列中，良好的散列函数对于使用键有效存储和检索元素至关重要。一个好的哈希函数应该易于在 O(1) 时间内计算，并在哈希表中均匀分布键。这被称为 散列均匀假设 ,它指出每个键同样可能散列到散列表中 m 个槽中的任何一个。
参考
- Book: Algorithms by CLRS
- Book: Algorithms by Robert Sedgewick
- Book: Algorithm design manual by Steven Skiena