A-Star加入了启发式函数，使得路径搜索更为高效。本文讲解了A-Star算法的一些细节。

概述

A-Star的诉求是通过一定的启发式条件剪枝掉一定的搜索空间。考虑在二维网格中搜索两个点的最短路径。如果使用宽搜类算法，其搜索路径如图所示。

可以想见的是，如果在搜索过程加上终点位置这一信息之后，每个搜索点的位置就不再平等，距离终点的终点距离更近的点成为了更好的点，如果可以优先搜索这些点，那么可以更快的搜索到终点。

基于这样的思想A-Star算法便诞生了。观察其搜索路径图示。

估计函数

考虑这样细节:

• 因为障碍的存在，我们不能准确估计哪些点是搜索终点更近的
  • 视觉上更近的点在搜索路劲中可能更远

正如这一节的标题，对于距离搜索终点的距离是一种估计。

估价的细节

估价函数有这样一些要求

1. 搜索目标点必须是存在，换言之，这个搜索过程必须是有解的。
2. 估价函数的取值范围需要满足该不等式
   • 真实值 >= 估计值 >= 0
3. 估价函数需要反应真实的单调性常见的估价函数设计思路
   • 基于距离 比如曼哈顿距离 欧式距离 对角距离
   • 基于真实的最短距离

算法过程

• 同时计算当前的搜索距离(成本)D和距离终点的估价距离F。这二者的和反应了路径的估计总成本。
• 维护一个优先队列，每次弹出路径估计总成本最低的节点出队，更新其他节点的距离。
• 当搜索终点第一次出队时，结束搜索，这时的路径为最短路径。

相关证明

正确性

证 : 第一次搜索到终点为最优路径。

• 假设第一次搜索到终点e不为最优，那么现在搜索路径中存在某个待选点 w , 经过w的路径是最优的真实路径。
  • 则 D(e) + F(e) >= real(d) >= D(w) + F(w)
• 那么便推出了矛盾，w应该先于e出队

图解

考虑这样的情况

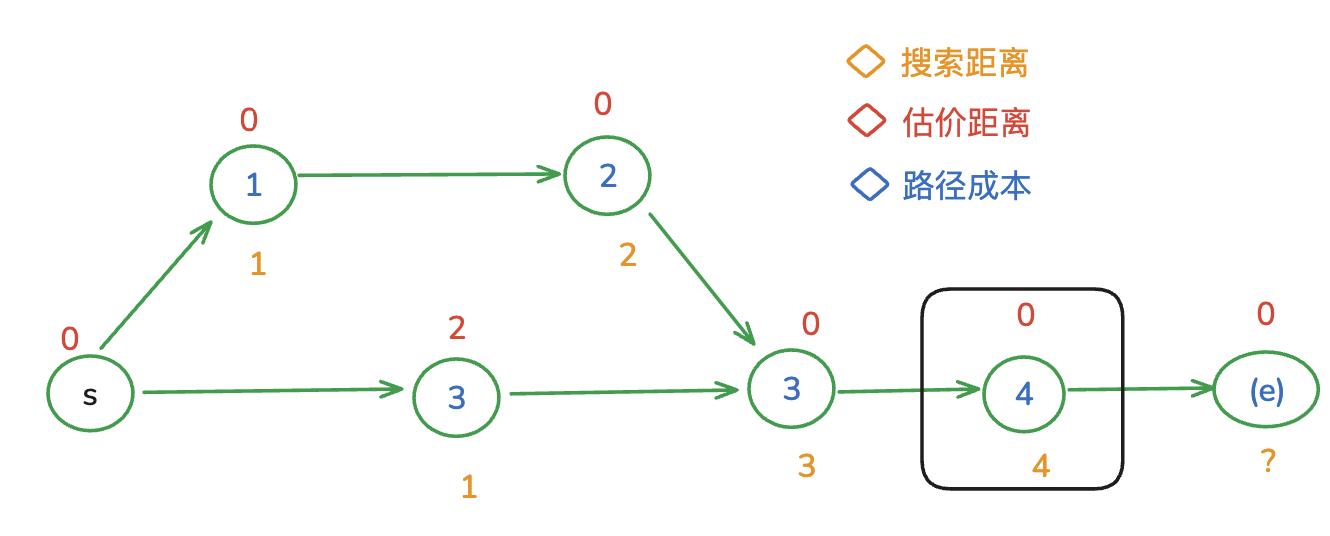路径会在框示节点回溯，从起点的右侧节点开始重新更新底侧路径的搜索距离。

对于其他节点，第一次搜索到并不一定是最小的。 终点搜索正确性是由估价函数的取值范围来保证的。

例题

Acwing 179 八数码

#include<iostream>
#include<map>
#include<queue>
#include<string>
#include<map>
#include<algorithm>
#include<utility>

using namespace std;
typedef pair<int , string> PII;

// 由于每次只移动一个节点 所以可以使用曼哈顿距离来进行估价
int cal(string state)
{
    int res = 0;
    for (int i = 0; i < state.size(); i ++ )
        if (state[i] != 'x')
        {
            int t = state[i] - '1';
            res += abs(i / 3 - t / 3) + abs(i % 3 - t % 3);
        }
    return res;
}

string Astar(string start)
{
    priority_queue<PII , vector<PII> , greater<PII>> q;
    // 维护每个点的前置节点和对应的移动方式
    unordered_map<string , pair<string , char>> prev; 
    unordered_map<string , int> dist;
    string end = "12345678x";
    q.push({cal(start) + 0 , start}); dist[start] = 0;
    
    int tx[] = { 0 , 0 , 1 , -1 };
    int ty[] = { 1 , -1 , 0 , 0 };
    string ops = "rldu";
    
    while(q.size())
    {
        PII f = q.top(); q.pop();
        string state = f.second; int step = f.first;
        
        if(state == end) break; 
        
        int idx = state.find('x');
        int x = idx / 3 , y = idx % 3;
        
        string source = state;
        for(int i = 0 ; i <= 3 ; i++)
        {
            int nx  = x + tx[i] , ny = y + ty[i] , nidx = nx * 3 + ny;
            if(nx >= 0 && nx <= 2 && ny >= 0 && ny <= 2)
            {
                swap(state[idx] , state[nidx]);
                if(dist.count(state) == 0 || dist[state] > step + 1)
                {
                    dist[state] = step + 1;
                    prev[state] = { source , ops[i] };
                    q.push({dist[state] + cal(state) , state});
                }
                swap(state[idx] , state[nidx]);
            }
            
        }
    }
    
    string res = "";
    while(end != start)
    {
        res += prev[end].second;
        end = prev[end].first;
    }
    reverse(res.begin() , res.end());
    return res;
}


int main()
{
    string start , seq;
    char c;
    
    while(cin >> c)
    {
        start += c;
        if(c != 'x') seq += c;
    }

	// 求解逆序对
    int cnt = 0;
    for(int i = 0 ; i < 8 ; i++)
        for(int j = i ; j < 8 ; j++)
            if(seq[j] > seq[i]) cnt++;

	// 逆序对是偶次变换的 如果初始逆序对为奇数 则无解
    if(cnt % 2 == 1) {
        cout << "unsolvable";
        return 0;
    }
    
    cout << Astar(start);
}

178. 第K短路

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;

const int N = 1e3 + 10 , M = 2e4 + 10;
int h[N] , rh[N] , e[M] , w[M] , ne[M] , idx;
int dist[N] , inQ[N];
int cnt[N];

typedef pair<int , pair<int , int>> PIII;

void add(int h[] , int a , int b , int c)
{
    w[idx] = c; e[idx] = b; ne[idx] = h[a] ; h[a] = idx++;
}

void init()
{
    memset(h , -1 , sizeof h);
    memset(rh , -1 , sizeof rh);
    memset(dist , 0x3f , sizeof dist);
}


// 在方向图中求出终点到其他点的最短距离
void spfa(int start)
{
    queue<int> q; q.push(start);
    dist[start] = 0; inQ[start] = true;
    
    while(q.size())
    {
        int f = q.front(); q.pop(); inQ[f] = false;
        
        for(int i = rh[f] ; i != -1 ; i = ne[i])
        {
            int j = e[i];
            
            if(dist[j] > dist[f] + w[i])
            {
                dist[j] = dist[f] + w[i];
                if(!inQ[j])
                {
                    q.push(j) ; inQ[j] = true;
                }
            }
        }
    }
}

int Astar(int s , int end , int k)
{
    priority_queue<PIII , vector<PIII> , greater<PIII>> heap;
    heap.push({0 + dist[s] , {0 , s}}); 
    
    while(heap.size())
    {
        auto t = heap.top(); heap.pop();
        int vertex = t.second.second , distance = t.second.first;
        
        cnt[vertex] ++;
        // 第一次访问终点 k 次是即为答案
        if(cnt[end] == k) return distance;
        
        // 入队所有可能的点
        for(int i = h[vertex] ; i != -1 ; i = ne[i])
        {
            int j = e[i];
            
            // 如果一个点已经被访问了超过 k 次 那么它不可能在 通往终点的 k 短路上
            if(cnt[j] <= k)
                heap.push({distance + dist[j] + w[i] , {distance + w[i] , j}});
        }
    }
    
    return -1;
}
int main()
{
    init();
    
    int n , m; cin >> n >> m;
    while(m --)
    {
        int a , b , c; cin >> a >> b >> c;
        add(h , a , b , c); add(rh , b , a , c);
    }
    
    int s , t , k; cin >> s >> t >> k;
    
    spfa(t);
    
    if(s == t) k ++; // 如果起点等于终点 因为是至少需要经过一条边 所以多一条路径
    
    cout << Astar(s , t , k);
}