本篇文章讲述了双向宽搜的思想，并且结合例题讲解编码实现方式。

思想

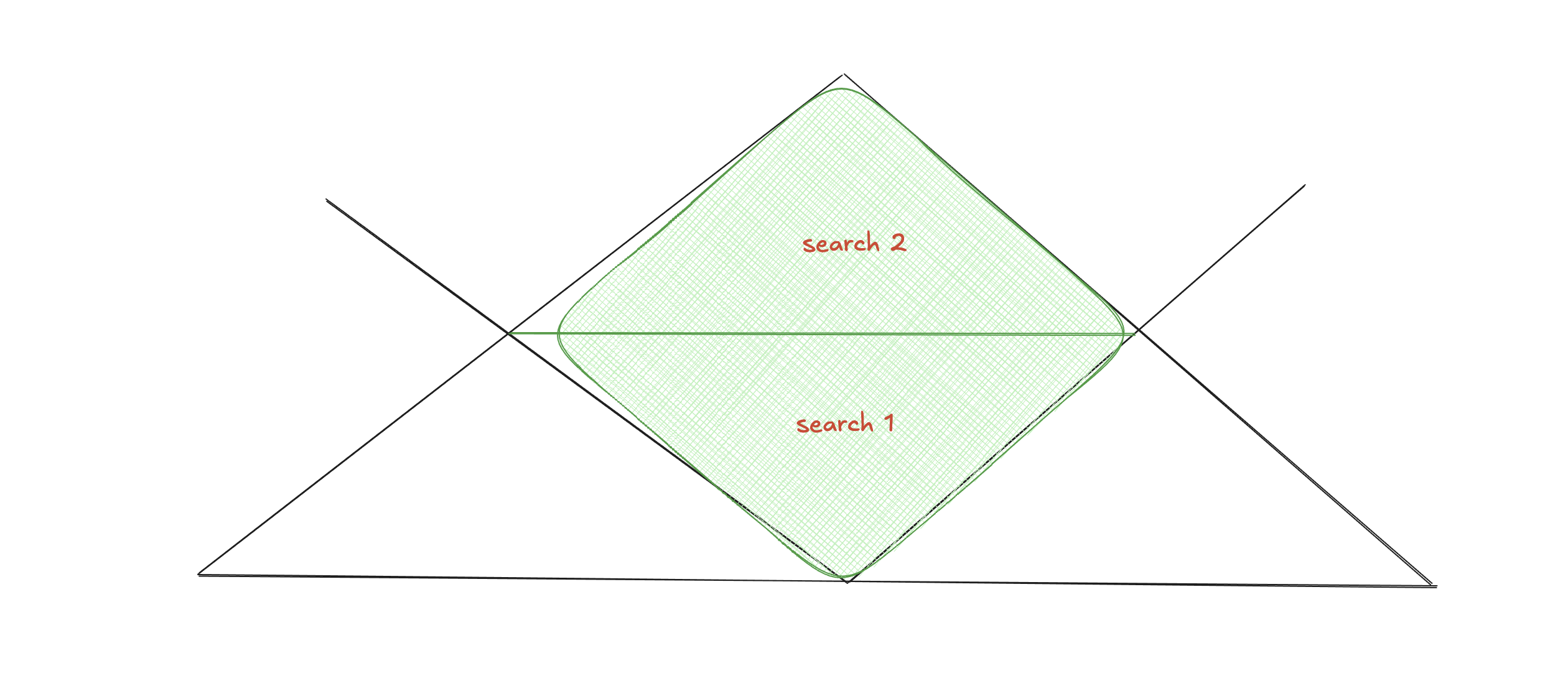
双向宽搜的思想是利用空间换时间，将整个搜索空间分为两部分，搜索一部分的结果保存起来，并且根据可能的条件做一些预处理。之后再去搜索另一半边。

假设我们的搜索节点是n, 在每个节点上二分支。原始的暴搜的复杂度是 O(2^n)。如果使用双端搜索复杂度降为O(2 ^ (n / 2) * A + 2 ^ (n / 2) * B)，A , B是操作常数。

如果 n == 46 可以将算法复杂度从 10^12降低到10^7。

例题

Acwing171 送礼物

#include<iostream>
#include<algorithm>

using namespace std;
int w , n; 
int items[50]; // 物品
int weights[1 << 24] , cnt; 
long long res;

// 枚举前一半物品所有可能的重量取值
// 将结果填到weights数组中
void dfs1(int u , long long load ,  int limit)
{
    if(u == limit) { weights[cnt ++] = load; return; }

	// 对于每个物品 枚举选或者不选
    if(items[u] + load <= w) dfs1(u + 1 , load + items[u] , limit);
    dfs1(u+1 , load , limit); 
}

// 枚举后一半物品所有可能的重量取值
void dfs2(int u , long long load)
{
    if (u == n) 
    {
	    // 对于一种可能的取值 找满足 weight[i] + load < w 的最大组合
	    // 并用这个组合尝试更新答案记录
        int l = 0 , r = cnt - 1;
        while(l < r)
        {
            int mid = (r + l + 1) / 2;
            if(weights[mid] + load <= w) l = mid;
            else r = mid - 1;
        }

		// 考虑二分答案不存在的情况
        if (weights[l] + load <= w) res = max(res , weights[l] + load);
        return;
    }

	// 对于每个物品 枚举选或者不选
    if (items[u] + load <= w) dfs2(u + 1 , load + items[u]);
    dfs2(u + 1 , load);
}

int main()
{
    cin >> w >> n;
    for(int i = 0 ; i < n ; i ++) cin >> items[i];

	// 排序 使得数字尽量靠近
	// 这样可以在去重时去掉更多重复情况 使weights中的记录更少
    sort(items , items + n);
    reverse(items , items + n);
    
    int seg = n / 2;
    dfs1(0 , 0 , seg);

	// 去重 weights
    sort(weights , weights + cnt);
    cnt = unique(weights , weights + cnt) - weights;
    
    dfs2(seg , 0);
    
    cout << res << endl;
}