ID-A*
本文讲解了 Iteration Deepen 和 A-star算法的结合使用，简称ID-A* 算法，本质上是一系列剪枝策略的集合。Iteration Deep可以控制每一轮搜索的最大迭代次数，防止搜索陷入到很深的分支中。A-star提供启发式估价函数，可以帮助提前结束当前的搜索分支。
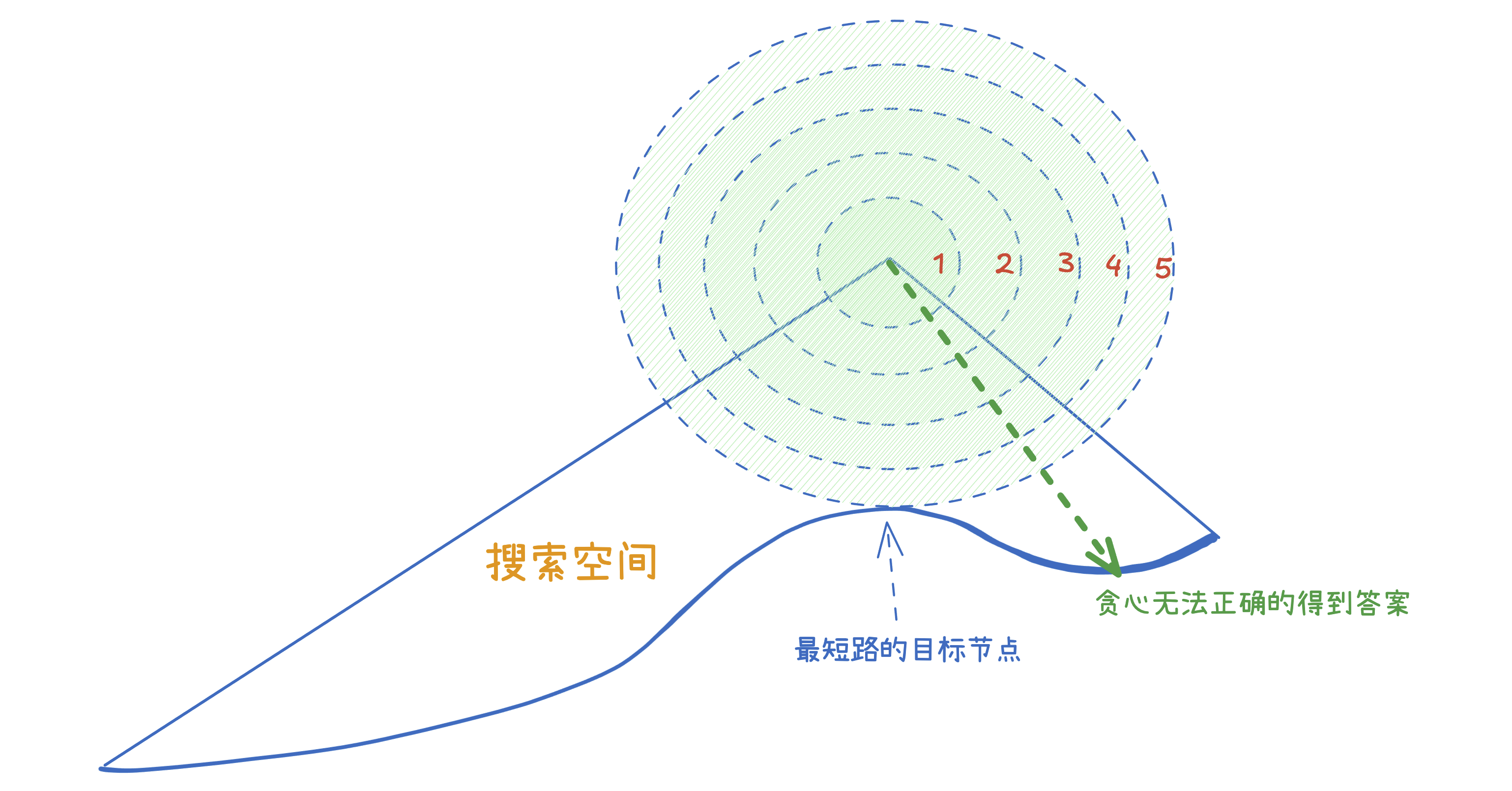
迭代加深
迭代加深控制每一轮的搜索轮次。其适合这样的情况：
- 搜索的目标存在于较浅的迭代轮次中
- 因为在每个节点的搜索分支多，导致使用宽搜需要维护过多的历史搜索结果。
- 如果需要推进搜索，需要全量维护上一层次
- 如果需要输出搜索路径，需要维护所有的层次
- 该问题没有一个正确的贪心解，使用贪心策略会陷入局部最优认为得到了一个正确解。
搜索轮次从 0 开始，第一次找到的结果的搜索轮次也是起点到重点的最短搜索路径(之一)。
例题
#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int path[N] , cnt = 1;
int n;
bool dfs(int u , int k)
{
if(u == k) return path[u-1] == n;
bool st[N] = {0,};
// 枚举所有可能的转移状态
for(int i = u-1 ; i >= 0 ; i--)
{
for(int j = i ; j >= 0 ; j--)
{
// 根据实际的题目的条件进行剪枝
int t = path[i] + path[j];
if(t > n || t < path[u-1] || st[t]) continue;
st[t] = 1;
path[u] = t;
// 如果当前的所有转移有任意一条可以到达目标位置 即返回true
if(dfs(u+1 , k)) return true;
}
}
return false;
}
int main()
{
path[0] = 1;
while(cin >> n , n)
{
// 不断增加迭代次数的上限 当一次dfs()返回 true时
// 得到起始状态到目标装提的最短路径
int k = 1;
while(!dfs(1 , k)) k++;
for(int i = 0 ; i < k ; i++)
cout << path[i] << " ";
cout << endl;
}
}ID-A*
算法思想非常简单，在执行ID的同时进行估价，如果发现当前状态在限制轮次前没有可能到达搜索目标，则提前结果搜索。
估价函数的设计要求和A-star算法中一致。Real() >= F() >= 0。这样一来
- 当 当前的搜索成本 + 估价成本 > 搜索限制时，真实的搜索路径也必定大于限制
- 当
F() == 0成立时，也意味着搜索到目标状态
例题
#include<iostream>
#include<string>
using namespace std;
// 估价函数 每次移动最多改变三个点后续节点
// 也即 每次移动最多可以修复三个点
// 以最好情况进行估计 当前距离目标状态的搜索的次数最少是 ceil(错误后续数量 / 3)
int cal(string state)
{
int cnt = 0;
for(int i = 1 ; i < state.length() ; i ++)
if(state[i] != state[i-1] + 1)
cnt ++;
return (cnt + 2) / 3;
}
bool dfs(string state , int level , int limit)
{
// 判断搜索成功和提前退出
if (cal(state) == 0) return true;
if (level + cal(state) > limit) return false;
// 枚举所有可能的转移
// 因为本质是交换两块区域 所以只需要枚举向后的情况即可
for(int start = 0 ; start < state.length() ; start ++)
{
for (int length = 1 ; length + start - 1 < state.length() ; length ++ )
{
string out = state.substr(start , length);
string nstate = state.substr(0 , start) + state.substr(start + length , -1);
string to;
for(int i = start + 1 ; i <= nstate.length() ; i++)
{
if (i == nstate.length())
{
to = nstate + out;
}
else
{
string l = nstate.substr(0 , i) , r = nstate.substr(i , -1);
to = l + out + r;
}
if (to == state) continue;
if (dfs(to , level + 1 , limit)) return true;
}
}
}
return false;
}
int main()
{
int T ; cin >> T;
while(T --)
{
int n ; cin >> n ;
string start ; int ch;
while(n-- && cin >> ch) start += 'a' + ch - 1;
int k = 0;
while(k < 5 && !dfs(start , 0 , k)) k ++;
if (k == 5) cout << "5 or more" << endl;
else cout << k << endl;
}
}版权所有
版权归属：