C++

Bit Operation in C++.

About 930 wordsAbout 3 min

语法位运算

2024-1-23

cover
本文介绍了c++整数存储和位运算符

二进制数

在计算机存储中，所有的数据在最底层都是以二进制的形式存储的。这和存储器件的物理特性有关系，对应了物理位单元的高低电平的状态。依据存储器类型( SRAM , DRAM , Hard Disk , Solid State Disk ....)不同，其底层的储层原理也不同，这里不做重点讨论。

而通过简单的数学计算，我们可以得到二进制数和十进制数之间的关系。例如

  0b(0 0011) = (5)d

  0b(1 0111) = (-7)d

这其中，0b 是二进制数前缀 , 二进制数第一位是符号位 0 / 1 分别代表 + / - 。d 是十进制后缀。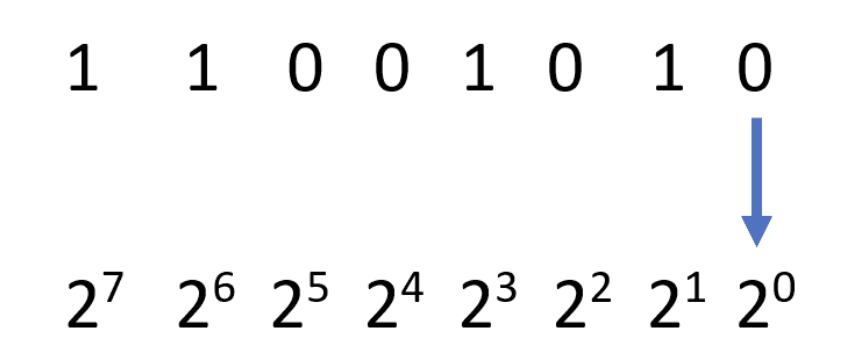

int 数据的存储方式

在 c++ 中, 整型包括

short (2 字节)
int (4 字节)
long (4 字节)
long long (8 字节)

括号给出了他们的最低字节数。在上一节中提到二进制与十进制转化中，得到是二进制数的原码。而计算机存储器件在存储一个具体二进制数时，使用的二进制的补码。

原码和补码之间有如下的转换规则：

对于正数和零，其补码就等于原码。
```
  (5)d = 0b(0 0011)原 = 0b(0 0011)补
```

对于负数，其补码等于该数按位取反(除了符号位)再加上 1。

  (-5)d = 0b(1 0011)原 = ob(1 1101)补

 0b(1 0011)原 —> 0b(1 1100)反 —> ob(1 1101)补

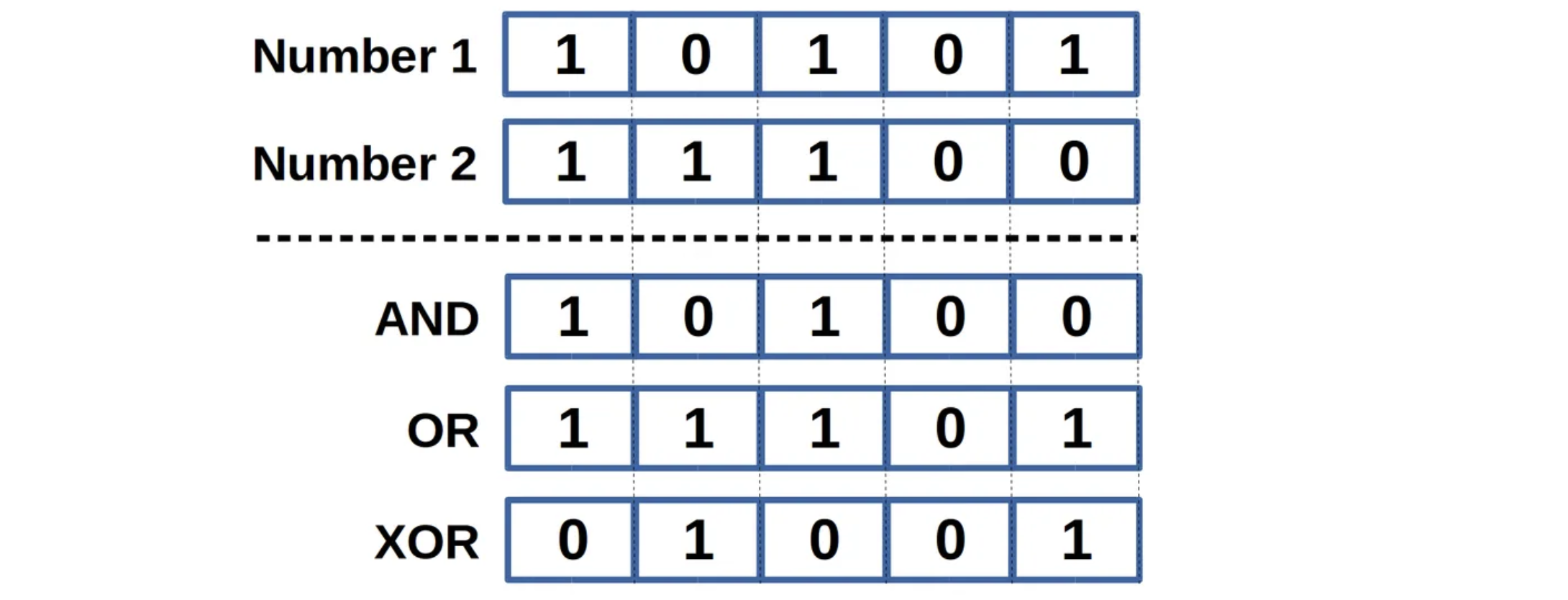
c++ 位运算符

c++提供了下面这些操作来支持我们对二进制数的位(bit)进行操作。

假定存在下面两个变量用来举例

A = 0b(0011 1100) = (60)d

B = 0b(0000 1101) = (13)d

运算符	描述	例子
&	按位与操作，按二进制位进行"与"运算。运算规则： 0 & 0= 0 0 & 1 = 0 1 & 0 = 0 1 & 1 = 1 可以类别逻辑运算符 and(&&)。	(A & B) 将得到 12。即为 0000 1100。
\|	按位或操作，按二进制位进行"或"运算。运算规则: 0 \| 0 = 0 0 \| 1 = 1 1 \| 0 = 1 1 \| 1 = 1 可以类别逻辑运算符 or(\|\|)。	(A \| B) 将得到 61。即为 0011 1101。
^	异或操作，按二进制位进行"异或"运算。运算规则： 0 ^ 0 = 0 0 ^ 1 = 1 1 ^ 0 = 1 1 ^ 1 = 0 相同位零，不同为 1。	(A ^ B) 将得到 49。即为 0011 0001。
~	取反运算符，按二进制位进行"取反"运算。运算规则： ~1= 0 ~0 = 1。	(~A ) 将得到 -61。即为 1100 0011。
>>	二进制左移运算符。将一个运算对象的各二进制位全部左移若干位。左边的二进制位丢弃，右边补 0。	A << 2 将得到 240，即为 1111 0000 相当于 * 4。
<<	二进制右移运算符。将一个数的各二进制位全部右移若干位。正数左补 0，负数左补 1，右边丢弃。	A >> 2 将得到 15，即为 0000 1111 相当于 / 4。

例子.二进制中一的个数

问题描述

给定一个长度为 n 的数列，请你求出数列中每个数的二进制表示中 1 的个数。

1≤n≤100000。0≤ 数列中元素的值 ≤10^9。

#include<iostream>
using namespace std;

// 不断向右移位 并和1 按位于直到这个数为零。
int bitCount(int n)
{
    int res = 0;
    while(n)
    {
        res += n & 1;
        n >>= 1;
    }
    return res;
}

int main()
{
    int n; cin >> n;
    while(cin >> n) printf("%d " , bitCount(n));
}